(本小题满分12分)
设函数f(x)=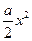 +
+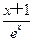 -1.
-1.
(1)若x≥0时,f(x)≥0恒成立,求a的取值范围;
(2)求证:对于大于1的正整数n,恒有1+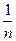 <
<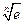 <1+
<1+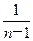 成立.
成立.
(本小题满分8分)
已知直线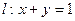 与椭圆
与椭圆 (
( 为参数),若直线
为参数),若直线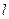 与椭圆交于A,B两点,求线段AB的长度。
与椭圆交于A,B两点,求线段AB的长度。
(满分10分)已知数列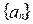 ,
,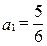 ,若以
,若以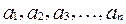 为系数的二次方程
为系数的二次方程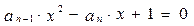 都有根
都有根 ,且满足
,且满足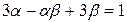 。
。
(1)求数列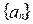 通项公式;
通项公式;
(2)求数列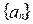 前
前 项和
项和 .
.
(满分12分)甲、乙两名同学在高一学年中(相同条件下)都参加数学考试十次,每次考试成绩如下表:
 次 次 数 数同学 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
| 甲 |
90 |
50 |
70 |
80 |
70 |
60 |
80 |
60 |
70 |
70 |
| 乙 |
20 |
40 |
60 |
80 |
70 |
70 |
80 |
90 |
90 |
100 |
请在坐标系中画出甲、乙两同学的成绩折线 图,并
图,并 从以下不同角度对这次测试结果进行分析。
从以下不同角度对这次测试结果进行分析。
(1)从平均数和方差相结合看,分析谁的成绩更稳定些;
(2)从平均数和中位数相结合看,分析谁的成绩好些;
(3)从平均数和成绩为90分以上的次数相结合看,分析谁的成绩好些 ;
(4)从折线图上两人成绩分数的走势看,分析谁更有潜力。
(满分9分)盒子中 有大小形状相同的4只红球、2只黑球,每个球被摸到的机会均等,求下列事件的概率:
有大小形状相同的4只红球、2只黑球,每个球被摸到的机会均等,求下列事件的概率:
(1)A=“任取一球,得到红球”;
(2)B=“ 任取两球,得到同色球”;
任取两球,得到同色球”;
(3)C=“任取三球,至多含一黑球”。
(满分10分)用自然语言设计一种计算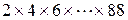 的值的算法,并画出相应的程序框图。
的值的算法,并画出相应的程序框图。