（本小题满分12分）
已知向量a=(1，1)，b=(1，0)，c满足a·c=0，且|a|=|c|，b·c>0
(1)求向量c；
(2)若映射f：(x，y)→(x′，y′)=xa+yc；
①求映射f下(1，2)的原象；
②若将(x，y)作点的坐标，问是否存在直线
使得直线上任一点在映射f的作用下，仍在直线上，若存在求出的方程，若不存在说明理由.
设△ABC的内角A，B，C所对的边长分别为a，b，c，m＝(cosA，cosC)，n＝(
c－2b，a)且m⊥n.
(1)求角A的大小；
(2)若角B＝
，BC边上的中线AM的长为
，求△ABC的面积.
已知函数f(x)=－x3＋3x2＋9x＋m
（I）求f(x)的单调递减区间；
（II）若f(x)在区间[－2，2]上的最大值为20，求它在该区间上的最小值．
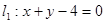直线
与直线
相交于点P，
求（1）过点P与直线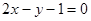
平行的直线方程；
（2）过点P与直线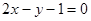垂直的直线方程。
在等差数列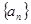
中，已知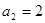
，
，
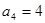（1）求数列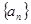的通项公式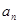
；
（2）设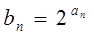
，求数列
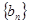前5项的和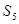
.
将进货单价为40元的仿古瓷瓶，按50元一个销售时能卖出500个．如果这类瓷瓶每个涨价1元时，销售量就减少10个．为了获取最大利润，售价应定为多少元？