(本小题满分12分)
某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本,分数频数分布如下表:
| 等级得分 |
 |
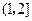 |
 |
 |
 |
 |
| 人数 |
3 |
17 |
30 |
30 |
17 |
3 |
(Ⅰ)如果以能力等级分数大于4分作为良好的标准,从样本中任意抽取2名学生,求恰有1名学生为良好的概率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为1.5)作为代表:
的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等 级分数的期望
级分数的期望 及标准差
及标准差 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在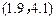 范围内的人数 .
范围内的人数 .
(Ⅲ)从这10000名学生中任意抽取5名同学,
他们数学与物理单科学习能力等级分
数如下表: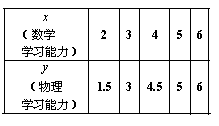
(ⅰ)请画出上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程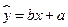 (附参考数据:
(附参考数据: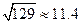 )
)
(本小题满分10分)
选修4-5:不等式选讲
设函数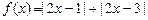 ,
,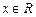 .
.
(1)解不等式: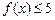 ;
;
(2)若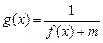 的定义域为
的定义域为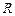 ,求实数
,求实数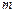 的取值范围.
的取值范围.
(本小题满分10分)
选修4-4:坐标系与参数方程选讲
已知曲线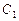 的参数方程为
的参数方程为 (
(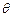 为参数),曲线
为参数),曲线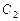 的参数方程为
的参数方程为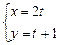 (
(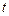 为参数).
为参数).
(1)若将曲线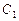 与
与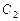 上各点的横坐标都缩短为原来的一半,分别得到曲线
上各点的横坐标都缩短为原来的一半,分别得到曲线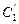 和
和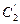 ,求出曲线
,求出曲线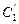 和
和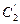 的普通方程;
的普通方程;
(2)以坐标原点为极点,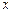 轴的非负半轴为极轴建立极坐标系,求过极点且与
轴的非负半轴为极轴建立极坐标系,求过极点且与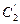 垂直
垂直 的直线的极坐标方程.
的直线的极坐标方程.
(本小题满分10分)
选修4-1:几何证明选讲
如图,已知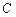 点在⊙
点在⊙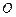 直径的延长线上,
直径的延长线上,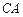 切⊙
切⊙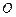 于
于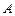 点,
点,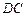 是
是 的平分线,且交
的平分线,且交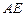 于
于 点,交
点,交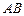 于
于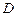 点.
点.
(1)求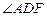 的度数;
的度数;
(2)若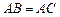 ,求
,求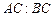 .
.
(本小题满分12分)
已知 ,
,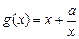
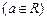 .
.
(1)求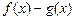 的单调区间;
的单调区间;
(2)若 时,
时,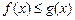 恒成立,求实数
恒成立,求实数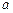 的取值范围;
的取值范围;
(本小题满分12分)
已知椭圆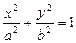 (
(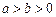 )的离心率为
)的离心率为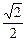 ,且短轴长为2.
,且短轴长为2.
(1)求椭圆的方程;
(2)若与两坐标轴都不垂直的直线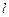 与椭圆交于
与椭圆交于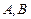 两点,
两点,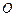 为坐标原点,且
为坐标原点,且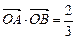 ,
,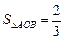 ,求直线
,求直线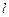 的方程.
的方程.