本小题满分10分)选修4—4:坐标系与参数方程
如图,已知点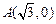 ,
, ,圆
,圆 是以
是以 为直径的圆,直线
为直径的圆,直线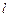 :
: (
( 为参数).
为参数).
(Ⅰ)写出圆 的普通方程并选取适当的参数改写为参数方程;
的普通方程并选取适当的参数改写为参数方程;
(Ⅱ)过原点 作直线
作直线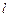 的垂线,垂足为
的垂线,垂足为 ,若动点
,若动点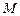 满足
满足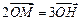 ,当
,当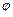 变化时,求点
变化时,求点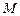 轨迹的参数方程,并指出它是什么曲线.
轨迹的参数方程,并指出它是什么曲线.
已知 为坐标原点,对于函数
为坐标原点,对于函数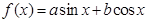 ,称向量
,称向量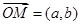 为函数
为函数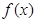 的伴随向量,设函数
的伴随向量,设函数 ,
,
(Ⅰ)求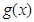 的伴随向量
的伴随向量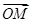 的模;
的模;
(Ⅱ)若 =
=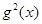 ,求
,求 在
在 内的最值及对应x的值.
内的最值及对应x的值.
已知函数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时有
时有 .
.
(1)判断函数 的单调性,并求使不等式
的单调性,并求使不等式 成立的实数
成立的实数 的取值范围.
的取值范围.
(2)若 、
、 、
、 分别是
分别是 的三个内角
的三个内角 、
、 、
、 所对的边,
所对的边, 面积
面积 求
求 、
、 的值;
的值;
设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若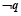 是
是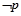 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.
(本小题满分14分)已知函数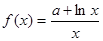 在点
在点 处的切线与
处的切线与 轴平行.
轴平行.
(1)求实数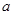 的值及
的值及 的极值;
的极值;
(2)是否存在区间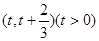 ,使函数
,使函数 在此区间上存在极值和零点?若存在,求实数
在此区间上存在极值和零点?若存在,求实数 的取值范围,若不存在,请说明理由;
的取值范围,若不存在,请说明理由;
(3)如果对任意的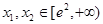 ,有
,有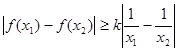 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数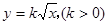 的一部分,后一段DBC是函数
的一部分,后一段DBC是函数 时的图象,图象的最高点为
时的图象,图象的最高点为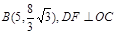 ,垂足为F.
,垂足为F.
(1)求函数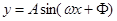 的解析式;
的解析式;
(2)若在草坪内修建如图所示的儿童游乐园PMFE,问点P落在曲线OD上何处时,儿童乐园的面积最大?