在“环境保护低碳生活知识竞赛”第一环节测试中，设有A、B、C三道必答题，分值依次为20分、30分、50分．竞赛规定：若参赛选手连续两道题答题错误，则必答题总分记为零分；否则各题得分之和记为必答题总分已知某选手回答A、B、C三道题正确的概率分别为
、
、
，且回答各题时相互之间没有影响．
(I)若此选手按A、B、C的顺序答题，求其必答题总分不小于80分
的概率；
(Ⅱ)若此选手可以自由选择答题顺序，求其必答题总分为50分的概率．
在平面直角坐标系xOy中，点B与点A（-1,1）关于原点O对称，P是动点，且直线AP与BP的斜率之积等于
.(Ⅰ)求动点P的轨迹方程；
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，说明理由。
设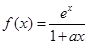
，其中
为正实数
（Ⅰ）当
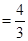时，求
的极值点；
（Ⅱ）若为
上的单调函数，求的取值范围。
已知函数
的图象与
在原点相切，且函数的极小值为
，（1）求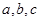
的值；（2）求函数的递减区间．
设命题
：函数
在
上递增；命题
：函数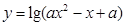
的定义域为R．若或为真，且为假，求
的取值范围．
的三个顶点为
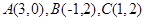，求：
（Ⅰ）BC边上的中线AD所在直线的方程；（Ⅱ）的外接圆方程。