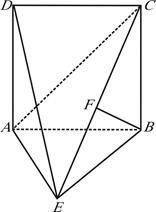
如图,已知菱形 的边长为
的边长为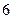 ,
,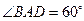 ,
,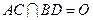 .将菱形
.将菱形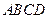 沿对角线
沿对角线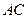 折起,使
折起,使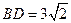 ,得到三棱锥
,得到三棱锥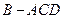 .
.
(Ⅰ)若点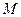 是棱
是棱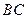 的中点,求证:
的中点,求证: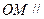 平面
平面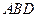 ;
;
(Ⅱ)求二面角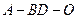 的余弦值;
的余弦值;
(Ⅲ)设点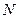 是线段
是线段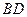 上一个动点,试确定
上一个动点,试确定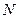 点的位置,使得
点的位置,使得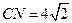 ,并证明你的结论
,并证明你的结论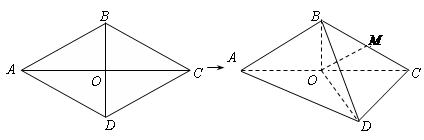
.(本小题满分13分)
已知数列 是其前
是其前 项和,且
项和,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 是数列
是数列 的前
的前 项和
项和 ,求T10的值
,求T10的值
(本小题满分12分)已知函数 (
( >0),若函数
>0),若函数 的最小正周期为
的最小正周期为 .
.
(1)求 的值,并求函数
的值,并求函数 的最大值
的最大值
(2)若0<x< ,当f(x)=
,当f(x)= 时,求
时,求 的值
的值
(本小题满分14分)
已知函数f(x)=-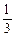 x3+bx2+cx+bc,
x3+bx2+cx+bc,
(1)若函数f(x)在x=1处有极值-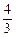 ,试确定b、c的值;
,试确定b、c的值;
(2)在(1)的条件下,曲线y=f(x)+m与x轴仅有一个交点,求实数m的取值范围;
(3)记g(x)=|f′(x)|(-1≤x≤1)的最大值为M,若M≥k对任意的b、c恒成立,试求k的取值范围.
(参考公式:x3-3bx2+4b3=(x+b)(x-2b)2)
(本小题满分14分)
已知椭圆G与双曲线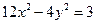 有相同的焦点,且过点
有相同的焦点,且过点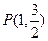 .
.
(1)求椭圆G的方程;
(2)设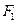 、
、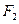 是椭圆G的左焦点和右焦点,过
是椭圆G的左焦点和右焦点,过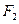 的直线
的直线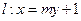 与椭圆G相交于A、B两点,请问
与椭圆G相交于A、B两点,请问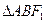 的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线
的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
(本小题满分14分)
如图,直二面角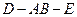 中,四边形
中,四边形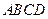 是正方形,
是正方形,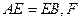 为CE上的点,且
为CE上的点,且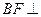 平面
平面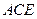 .
.
(1)求证: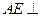 平面
平面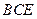 ;
;
(2)求二面角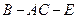 的余弦值.
的余弦值.