(本小题满分12分)已知函数 (
( >0),若函数
>0),若函数 的最小正周期为
的最小正周期为 .
.
(1)求 的值,并求函数
的值,并求函数 的最大值
的最大值
(2)若0<x< ,当f(x)=
,当f(x)= 时,求
时,求 的值
的值
已知二次函数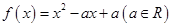 同时满足:
同时满足:
①不等式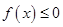 的解集有且只有一个元素;
的解集有且只有一个元素;
②在定义域内存在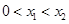 ,使得不等式
,使得不等式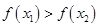 成立.
成立.
数列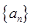 的通项公式为
的通项公式为 .
.
(1)求函数 的表达式;
的表达式;
(2)求数列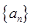 的前
的前 项和
项和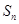 .
.
已知函数 ,
,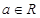 .
.
(1)当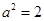 时,求
时,求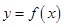 在
在 处的切线方程;
处的切线方程;
(2)若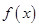 在
在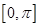 内单调递增,求
内单调递增,求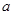 的取值范围.
的取值范围.
在锐角 内角
内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .已知
.已知 ,
,
 .
.
求:(1) 外接圆半径;
外接圆半径;
(2)当 时,求
时,求 的大小.
的大小.
已知函数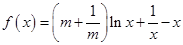 ,(其中常数
,(其中常数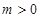 ).
).
(1)当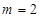 时,求
时,求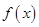 的极大值;
的极大值;
(2)试讨论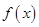 在区间
在区间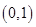 上的单调性;
上的单调性;
(3)当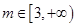 时,曲线
时,曲线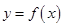 上总存在相异两点
上总存在相异两点 、
、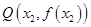 ,使得曲线
,使得曲线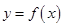 在点
在点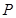 、
、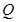 处的切线互相平行,求
处的切线互相平行,求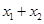 的取值范围.
的取值范围.
已知曲线 ,过
,过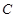 上一点
上一点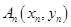 作一斜率为
作一斜率为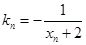 的直线交曲线
的直线交曲线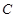 于另一点
于另一点 (
(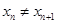 且
且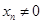 ,点列
,点列 的横坐标构成数列
的横坐标构成数列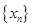 ,其中
,其中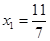 .
.
(1)求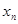 与
与 的关系式;
的关系式;
(2)令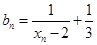 ,求证:数列
,求证:数列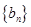 是等比数列;
是等比数列;
(3)若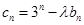 (
(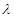 为非零整数,
为非零整数,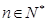 ),试确定
),试确定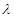 的值,使得对任意
的值,使得对任意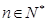 ,都有
,都有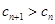 成立.
成立.