(本小题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班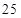 名女同学,
名女同学,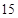 名男同学中随机抽取一个容量为
名男同学中随机抽取一个容量为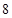 的样本进行分析.随机抽出
的样本进行分析.随机抽出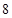 位,他们的数学分数从小到大排序是:
位,他们的数学分数从小到大排序是: 、
、 、
、 、
、 、
、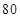 、
、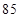 、
、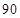 、
、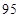 ,物理分数从小到大排序是:
,物理分数从小到大排序是: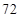 、
、 、
、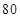 、
、 、
、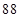 、
、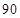 、
、 、
、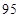 .
.
(Ⅰ)如果按性别比例分层抽样,男女同学分别抽取多少人?
(Ⅱ)若这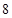 位同学的数学、物理分数对应如下表:
位同学的数学、物理分数对应如下表:
| 学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 数学分数x |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
| 物理分数y |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据用变量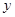 与
与 的相关系数或散点图说明物理成绩
的相关系数或散点图说明物理成绩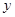 与数学成绩
与数学成绩 之间是否具有线性相关性?如果具有线性相关性,求
之间是否具有线性相关性?如果具有线性相关性,求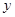 与
与 的线性回归方程(系数精确到
的线性回归方程(系数精确到 );如果不具有线性相关性,请说明理由.
);如果不具有线性相关性,请说明理由.
参考公式:相关系数 ;回归直线的方程是:
;回归直线的方程是: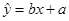 .
.
其中对应的回归估计值:
参考数据: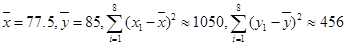 ,
, .
.
(本小题满分12分)在直角坐标系 中,以原点
中,以原点 为极点,
为极点, 轴的正半轴为极轴,建立极坐标系.已知曲线
轴的正半轴为极轴,建立极坐标系.已知曲线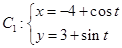 (
(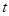 为参数),
为参数), (
( 为参数).
为参数).
(Ⅰ)化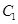 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若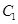 上的点
上的点 对应的参数为
对应的参数为 ,
,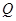 为
为 上的动点,求
上的动点,求 中点
中点 到直线
到直线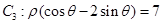 距离的最小值.
距离的最小值.
(本小题满分10分)某地对 人进行运动与性别是否有关测试,其中
人进行运动与性别是否有关测试,其中 名男性中有
名男性中有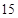 名喜欢运动,
名喜欢运动, 名女性中
名女性中 名喜欢运动.
名喜欢运动.
(Ⅰ)根据以上数据建立一个 列联表;
列联表;
(Ⅱ)判断喜欢运动是否与性别有关?
参考数据: .
.
临界值表:
 |
0.100 |
0.050 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分12分)
在平面直角坐标系 中,已知曲线
中,已知曲线 (
( 为参数),过点
为参数),过点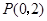 且斜率为
且斜率为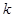 的直线与曲线
的直线与曲线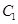 相交于不同的两点
相交于不同的两点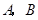 .
.
(Ⅰ)求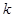 的取值范围;
的取值范围;
(Ⅱ)设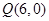 ,是否存在常数
,是否存在常数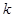 ,使得向量
,使得向量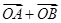 与
与 共线?如果存在,求
共线?如果存在,求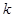 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
(本小题满分12分)已知函数
(Ⅰ)求函数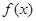 单调区间;
单调区间;
(Ⅱ)若 ,求证:当
,求证:当 时,
时, .
.