已知函数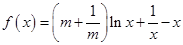 ,(其中常数
,(其中常数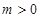 ).
).
(1)当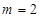 时,求
时,求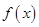 的极大值;
的极大值;
(2)试讨论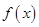 在区间
在区间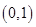 上的单调性;
上的单调性;
(3)当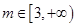 时,曲线
时,曲线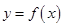 上总存在相异两点
上总存在相异两点 、
、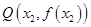 ,使得曲线
,使得曲线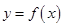 在点
在点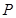 、
、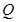 处的切线互相平行,求
处的切线互相平行,求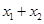 的取值范围.
的取值范围.
某蔬菜收购点租用车辆,将100t新鲜辣椒运往某市销售,可租用的大卡车和农用车分别为10辆和20辆,若每辆卡车载重8t,运费960元,每辆农用车载重2.5t,运费360元,据此,安排两种车型,应满足那些不等关系,请列出来.
某旅游公司年初以98万元购进一辆豪华旅游车,第一年各种费用为12万元,以后每年都增加4万元,该车每年的旅游效益为50万元,设第n年开始获利,列出关于n的不等关系.
某车间有20名工人,每人每天可加工甲种零件5件或乙种零件4件。在这20名工人中,派x人加工乙种零件,其余的加工甲种零件,已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元,若要使车间每天获利不低于1800元,写出x所要满足的不等关系.
将若干只鸡放入若干个笼,若每个笼里放4只,则有一鸡无笼可放:若每个笼里放5只,则有一笼无鸡可放。设现有笼x个,试列出x满足的不等关系,并说明至少有多少只鸡多少个笼?至多有多少只鸡多少个笼?
某次数学测验,共有16道题,答对一题得6分,答错一题倒扣2分,不答则不扣分,某同学有一道题未答,那么这个学生至少答对多少题,成绩才能在60分以上?列出其中的不等关系。