（本题12分）
为拉动经济增长，某市决定新建一批重点工程，分别为基础设施工程、民生工程和产业建设工程三类。这三类工程所含项目的个数分别为6，4，2。现在3名工人独立地从中任选一个项目参与建设。
（1）求他们选择的项目所属类别互不相同的概率；
（2）记
为3人中选择的项目属于基础设施工程或产业建设工程的人数，求的分布列及数学期望。
（本小题满分12分）已知函数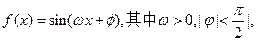
，且
，又知函数
（1）求
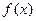的解析式；
（2）若将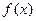的图象向右平移
个单位得到
的图象，求的单调递增区间。
（本小题满分12分）已知：数列
与—3的等差中项。（1）求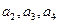
；（2）求数列
的通项公式。
设函数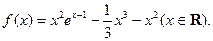
（1）求函数
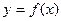的单调区间；（2）求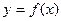在[—1，2]上的最小值；（3）当
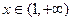时，用数学归纳法证明：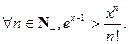
（本小题满分12分）已知定点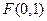
和直线
，过定点F与直线
相切的动圆圆心为点C。（1）求动点C的轨迹方程；（2）过点F在直线l2交轨迹于两点P、Q，交直线l1于点R，求
的最小值。
（本小题满分12分）济南市有大明湖、趵突泉、千佛山、园博园4个旅游景点，一位客人浏览这四个景点的概率分别是0.3，0.4，0.5，0.6，且客人是否游览哪个景点互不影响，设
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。（1）求=0对应的事件的概率；（2）求的分布列及数学期望。