泉州市为鼓励企业发展“低碳经济”,真正实现“低消耗、高产出”,施行奖惩制度.通过制定评
分标准,每年对本市 的企业抽查评估,评出优秀、良好、合格和不合格四个等次,
的企业抽查评估,评出优秀、良好、合格和不合格四个等次,
并根据等级给予相应的奖惩(如下表).某企业投入 万元改造,由于自身技术原因,
万元改造,由于自身技术原因,
能达到以上四个等次的概率分别为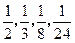 ,且由此增加的产值分别为
,且由此增加的产值分别为 万元、
万元、 万元、
万元、 万元、
万元、 万元.设该企业当年因改造而增加利润为
万元.设该企业当年因改造而增加利润为 .
.
(Ⅰ)在抽查评估中,该企业能被抽到且被评为合格以上等次的概率是多少?
(Ⅱ)求 的数学期望.
的数学期望.
| 评估得分 |
 |
 |
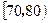 |
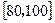 |
| 评定等级 |
不合格 |
合格 |
良好 |
优秀 |
| 奖惩(万元) |
 |
 |
 |
 |
已知 ,点
,点 在曲线
在曲线 上
上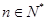 ,
, (Ⅰ)(Ⅰ)求数列
(Ⅰ)(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前n项和为
的前n项和为 ,若对于任意的
,若对于任意的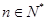 ,使得
,使得 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值.
如图,在四棱锥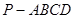 中,底面
中,底面 是矩形,
是矩形,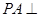 底面
底面 ,
, 是
是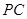 的中点,已知
的中点,已知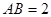 ,
, ,
,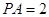 ,
,
求:(Ⅰ)三角形 的面积;(II)三棱锥
的面积;(II)三棱锥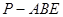 的体积
的体积
已知函数 ,若
,若 的最大值为1.
的最大值为1.
(1)求 的值,并求
的值,并求 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角 、
、 、
、 的对边
的对边 、
、 、
、 ,若
,若 ,且
,且 ,试判断三角形的形状.
,试判断三角形的形状.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组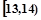 ;第二组
;第二组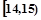 ,……,第五组
,……,第五组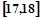 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图. 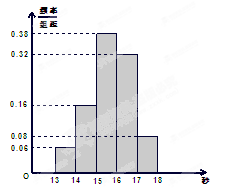
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设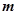 、
、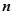 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知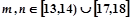 ,求事件“
,求事件“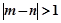 ”的概率.
”的概率.
已知函数f(x)=aex,g(x)=lnx-lna,其中a为常数,e=2.718…,且函数y=f(x)和y=g(x)的图像在它们与坐标轴交点处的切线互相平行.
(1)求常数a的值;(2)若存在x使不等式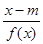 >
>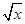 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)对于函数y=f(x)和y=g(x)公共定义域内的任意实数x0,我们把|f(x0)-g(x0)|的值称为两函数在x0处的偏差.求证:函数y=f(x)和y=g(x)在其公共定义域内的所有偏差都大于2.