某企业2010年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降。若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在 末扣除技术资金的情况下,第n年(2011年为第一年)的利润为500(1+
末扣除技术资金的情况下,第n年(2011年为第一年)的利润为500(1+ )万元(n为正整数)
)万元(n为正整数)
(1)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求 、
、 的表达式;
的表达式;
(2)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
(本小题满分14分)
已知椭圆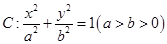 的离心率为
的离心率为 ,且经过点
,且经过点 .圆
.圆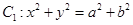 .
.
(1)求椭圆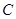 的方程;
的方程;
(2)若直线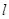
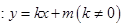 与椭圆C有且只有一个公共点
与椭圆C有且只有一个公共点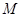 ,且
,且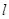 与圆
与圆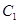 相交于
相交于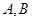 两点,问
两点,问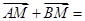
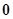 是否成立?请说明理由.
是否成立?请说明理由.
(本小题满分14分)
已知首项为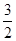 ,公比不等于
,公比不等于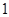 的等比数列
的等比数列 的前
的前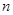 项和为
项和为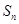 ,且
,且 ,
,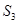 ,
,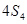 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,数列
,数列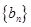 的前
的前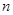 项和为
项和为 ,求证:
,求证:
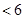 .
.
(本小题满分14分)
如图,在多面体 中,
中,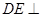 平面
平面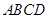 ,
,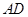 ∥
∥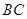 ,平面
,平面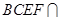 平面
平面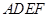
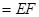 ,
, ,
,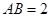 ,
, .
.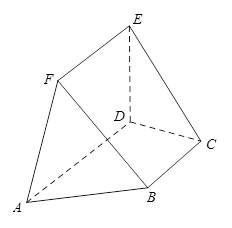
(1)求证: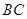 ∥
∥ ;
;
(2)求三棱锥 的体积.
的体积.
(本小题满分12分)
某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温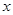 (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量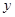 (杯),得到如下数据:
(杯),得到如下数据:
| 日期 |
1月11日 |
1月12日 |
1月13日 |
1月14日 |
1月15日 |
平均气温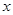 (°C) (°C) |
9 |
10 |
12 |
11 |
8 |
销量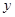 (杯) (杯) |
23 |
25 |
30 |
26 |
21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程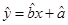 .
.
(参考公式: .)
.)
(本小题满分12分)
已知函数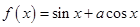
 R
R ,
, 是函数
是函数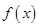 的一个零点.
的一个零点.
(1)求 的值,并求函数
的值,并求函数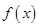 的单调递增区间;
的单调递增区间;
(2)若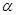
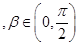 ,且
,且 ,
,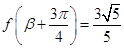 ,求
,求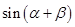 的值.
的值.