如图,圆O的半径OB垂直于直径AC,M为OA上一点,BM的延长线交圆O于N,过N点的切线交CA的延长线于P。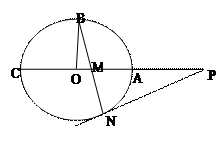
(1)求证: 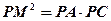 ;
;
(2)若圆O的半径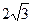 ,OA=
,OA= OM,求MN的长。
OM,求MN的长。
已知向量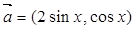
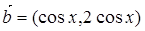
(1)求 并求
并求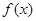 的单调递增区间。
的单调递增区间。
(2)若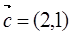 ,且
,且 与
与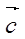 共线,
共线,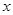 为第二象限角,求
为第二象限角,求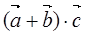 的值。
的值。
(本小题满分14分)已知函数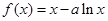 ,
,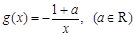 。
。
(1) 若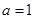 ,求函数
,求函数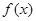 的极值;
的极值;
(2) 设函数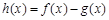 ,求函数
,求函数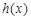 的单调区间;
的单调区间;
(3) 若在区间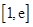 (
(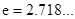 )上存在一点
)上存在一点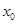 ,使得
,使得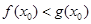 成立,求
成立,求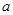 的取值范围。
的取值范围。
(本小题满分13分)设数列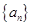 的前
的前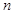 项和为
项和为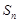 .已知
.已知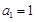 ,
,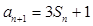 ,
,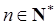 .
.
(1)写出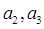 的值,并求数列
的值,并求数列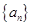 的通项公式;
的通项公式;
(2)记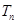 为数列
为数列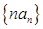 的前
的前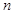 项和,求
项和,求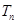 ;
;
(3)若数列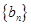 满足
满足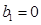 ,
,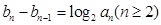 ,求数列
,求数列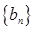 的通项公式.
的通项公式.
(本小题满分12分)已知二次函数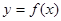 的图象过点(0,—3),且
的图象过点(0,—3),且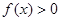 的解集(1,3)。
的解集(1,3)。
(1)求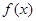 的解析式;
的解析式;
(2)若当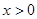 时,恒有
时,恒有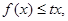 求实数t的取值范围。
求实数t的取值范围。
(本小题满分12分)若向量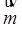
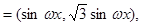
 =
= ,在函数
,在函数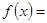
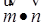 +
+ 的图象中,对称中心到对称轴的最小距离为
的图象中,对称中心到对称轴的最小距离为 ,且当
,且当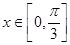 时,
时, 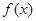 的最大值为
的最大值为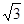 .
.
(1)求函数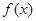 的解析式;
的解析式;
(2)求函数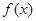 的单调递增区间.
的单调递增区间.