2010年度东风公司神鹰汽车改装厂开发出A型农用车,其成本价为每辆2万元,出厂价为每辆2.4万元,年销售价为10000辆,2011年为了支援西部大开发的生态农业建设,该厂抓住机遇,发展企业,全面提高A型农用车的科技含量,每辆农用车的成本价增长率为x,出厂价增长率为0.75x,预测年销售增长率为0.6x.(年利润=(出厂价-成本价)×年销售量)
(1)求2011年度该厂销售A型农用车的年利润y(万元)与x之间的函数关系。
(2)该厂要是2001年度销售A型农用车的年利润达到4028万元,该年度A型农用车的年销售量应该是多少辆?
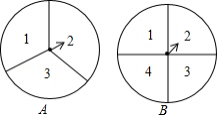
如图,转盘 的三个扇形面积相等,分别标有数字1,2,3,转盘 的四个扇形面积相等,分别有数字1,2,3,4.转动 、 转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.
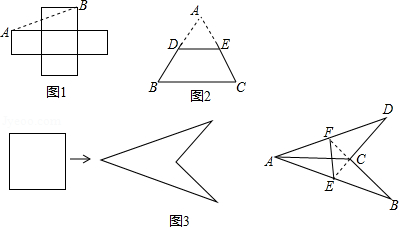
(1)阅读材料:
教材中的问题,如图1,把5个边长为1的小正方形组成的十字形纸板剪开,使剪成的若干块能够拼成一个大正方形,小明的思考:因为剪拼前后的图形面积相等,且5个小正方形的总面积为5,所以拼成的大正方形边长为 ,故沿虚线 剪开可拼成大正方形的一边,请在图1中用虚线补全剪拼示意图.
(2)类比解决:
如图2,已知边长为2的正三角形纸板 ,沿中位线 剪掉 ,请把纸板剩下的部分 剪开,使剪成的若干块能够拼成一个新的正三角形.
①拼成的正三角形边长为 ;
②在图2中用虚线画出一种剪拼示意图.
(3)灵活运用:
如图3,把一边长为 的正方形彩纸剪开,用剪成的若干块拼成一个轴对称的风筝,其中 ,延长 、 分别与 、 交于点 、 ,点 、 分别为 、 的中点,在线段 和 处用轻质钢丝做成十字形风筝龙骨,在图3的正方形中画出一种剪拼示意图,并求出相应轻质钢丝的总长度.(说明:题中的拼接都是不重叠无缝隙无剩余)
一只不透明的袋子中装有1个红球、1个黄球和1个白球,这些球除颜色外都相同
(1)搅匀后从袋子中任意摸出1个球,求摸到红球的概率;
(2)搅匀后从袋子中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球,求两次都摸到红球的概率.
为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成如下统计图.
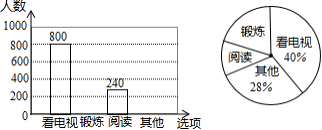
根据统计图所提供的信息,解答下列问题:
(1)本次共调查了 名市民;
(2)补全条形统计图;
(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数.
如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,抛物线经过点 和点 ,点 是第一象限抛物线上的一个动点.
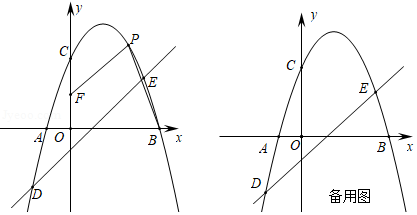
(1)求直线 和抛物线的表达式;
(2)在 轴上取点 ,连接 , ,当四边形 的面积是7时,求点 的坐标;
(3)在(2)的条件下,当点 在抛物线对称轴的右侧时,直线 上存在两点 , (点 在点 的上方),且 ,动点 从点 出发,沿 的路线运动到终点 ,当点 的运动路程最短时,请直接写出此时点 的坐标.