已知0<a<,A=1-a2,B=1+a2,C=,D=.
(1)求证:1-a>a2;
(2)比较A、B、C、D的大小
设函数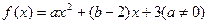 ,若不等式
,若不等式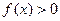 的解集为(-1,3)。
的解集为(-1,3)。
(1)求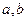 的值;
的值;
(2)若函数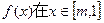 上的最小值为1,求实数
上的最小值为1,求实数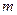 的值。
的值。
在 中,角
中,角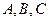 的对边分别为
的对边分别为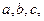 已知
已知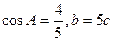 .
.
(1)求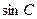 的值;
的值;
(2)若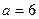 ,求
,求 的面积S的值。
的面积S的值。
已知定义在R上的函数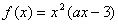 ,其中a为常数.
,其中a为常数.
(1)若x=1是函数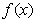 的一个极值点,求a的值;
的一个极值点,求a的值;
(2)若函数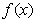 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(3)若函数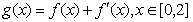 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.
已知数列{an}是首项为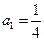 ,公比为
,公比为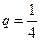 的等比数列,设
的等比数列,设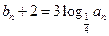 (n
(n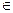 N*),数列{
N*),数列{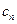 }满足
}满足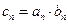
(1)求数列{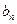 }的通项公式;
}的通项公式;
(2)求数列{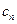 }的前n项和
}的前n项和
已知函数f(x)=cos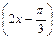 +2sin
+2sin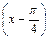 ·sin
·sin .
.
(1)求函数f(x)的最小正周期和图象的对称轴方程;
(2)求函数f(x)在区间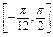 上的值域.
上的值域.