某商场预计全年分批购入每台价值为2 000元的电视机共3 600台,每批都购入x台(x为正整数),且每批需付运费400元,储存购入的电视机全年所付保管费用与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运费和保管费共43 600元.现全年只有24 000元资金可用于支付这笔费用.请问能否恰当地安排每批进货的数量,使资金够用?写出你的结论并说明理由.
(矩阵与变换)
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(Ⅰ) 求矩阵M; (Ⅱ) 设直线l在变换M作用下得到了直线m:x-y=4,求l的方程.
(本小题满分10分) 如图A,B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.现从中任取三条网线且使每条网线通过最大的信息量.
如图A,B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.现从中任取三条网线且使每条网线通过最大的信息量.
(1)设选取的三条网线由A到B可通过的信息
总量为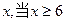 时,则保证信息畅通.
时,则保证信息畅通.
求线路信息畅通的概率;
(2)求选取的三条网线可通过信息总量的数学期望.
(本小题满分16分)
已知正三角形OAB的三个顶点都在抛物线 上,其中O为坐标原点,设圆C是
上,其中O为坐标原点,设圆C是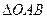 的外接圆(点C为圆心)(1)求圆C的方程;(2)设圆M的方程为
的外接圆(点C为圆心)(1)求圆C的方程;(2)设圆M的方程为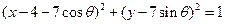 ,过圆M上任意一点P分别作圆C的两条切线PE、PF,切点为E、F,求
,过圆M上任意一点P分别作圆C的两条切线PE、PF,切点为E、F,求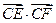 的最大值和最小值
的最大值和最小值
(本小题14分)设关于x的方程
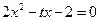 的两根为
的两根为 函数
函数 =
=
(1). 求f( 的值. (2).证明:
的值. (2).证明: 在[
在[ 上是增函数.(3).对任意正数
上是增函数.(3).对任意正数 ,求证:
,求证:
(本小题12分)设点 ,点A在y轴上移动,点B在x轴正半轴(包括原点)上移动,点M在AB连线上,且满足
,点A在y轴上移动,点B在x轴正半轴(包括原点)上移动,点M在AB连线上,且满足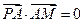 ,
, .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)设轨迹C的焦点为F,准线为l,自M引的垂线,垂足为N,设点 使四边形PFMN是菱形,试求实数a;
使四边形PFMN是菱形,试求实数a; (Ⅲ)如果点A的坐标为
(Ⅲ)如果点A的坐标为 ,
,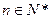 ,其中
,其中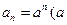 >
>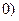 ,相应线段AM的垂直平分线交x轴于
,相应线段AM的垂直平分线交x轴于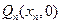 .设数列
.设数列 的前n项和为
的前n项和为 ,证明:当n≥2时,
,证明:当n≥2时, 为定值.
为定值.