已知离心率为的椭圆的中心在原点,焦点在x轴上.双曲线以椭圆的长轴为实轴,短轴为虚轴,且焦距为2.求椭圆及双曲线的方程
本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油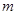 万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前
万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前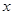 个月的需求量
个月的需求量 (万吨)与
(万吨)与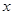 的函数关系为
的函数关系为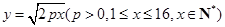 ,并且前4个月,区域外的需求量为20万吨.
,并且前4个月,区域外的需求量为20万吨.
(1)试写出第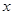 个月石油调出后,油库内储油量
个月石油调出后,油库内储油量 (万吨)与
(万吨)与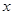 的函数关系式;
的函数关系式;
(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定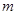 的取值范围.
的取值范围.
本题共有2个小题,第(1)小题满分4分,第(2)小题满分10分.
设三角形 的内角
的内角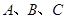 所对的边长分别是
所对的边长分别是 ,且
,且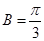 .若
.若 不是钝角三角形,求:
不是钝角三角形,求:
(1)角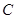 的范围;
的范围;
(2) 的取值范围.
的取值范围.
如图,已知圆锥的底面半径为 ,点Q为半圆弧
,点Q为半圆弧 的中点,点
的中点,点 为母线
为母线 的中点.若直线
的中点.若直线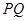 与
与 所成的角为
所成的角为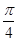 ,求此圆锥的表面积.
,求此圆锥的表面积.
本题共有3个小题,第(1)小题满分4分,第(2)小题满分7分,第(3)小题满分7分.
各项均为正数的数列 的前
的前 项和为
项和为 ,且对任意正整数
,且对任意正整数 ,都有
,都有 .
.
(1)求数列 的通项公式;
的通项公式;
(2)如果等比数列 共有
共有 项,其首项与公比均为
项,其首项与公比均为 ,在数列
,在数列 的每相邻两项
的每相邻两项 与
与 之间插入
之间插入 个
个 后,得到一个新的数列
后,得到一个新的数列 .求数列
.求数列 中所有项的和;
中所有项的和;
(3)如果存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的范围.
的范围.
本题共有3个小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分6分.
已知两动圆 和
和 (
( ),把它们的公共点的轨迹记为曲线
),把它们的公共点的轨迹记为曲线 ,若曲线
,若曲线 与
与 轴的正半轴的交点为
轴的正半轴的交点为 ,且曲线
,且曲线 上的相异两点
上的相异两点 满足:
满足: .
.
(1)求曲线 的方程;
的方程;
(2)证明直线 恒经过一定点,并求此定点的坐标;
恒经过一定点,并求此定点的坐标;
(3)求 面积
面积 的最大值.
的最大值.