已知圆C:x2+y2=r2(r>0)经过点(1,).
(1)求圆C的方程;
(2)是否存在经过点(-1,1)的直线l,它与圆C相交于A,B两个不同点,且满足=+(O为坐标原点)关系的点M也在圆C上?如果存在,求出直线l的方程;如果不存在,请说明理由.
已知数列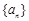 的前n项和
的前n项和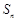 ,满足:
,满足: 三
三
点共线(a为常数,且 ).
).
(Ⅰ)求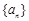 的通项公式;
的通项公式;
(Ⅱ)设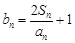 ,若数列
,若数列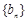 为等比数列,求a的值;
为等比数列,求a的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设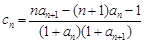 ,数列
,数列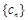 的前n项和为
的前n项和为 ,是否存在最小的整数m,使得任意的n均有
,是否存在最小的整数m,使得任意的n均有 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知向量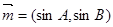 ,
,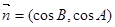 ,若
,若 ,
,
且 、
、 、
、 分别为
分别为 的三边
的三边 、
、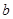 、
、 所对的角.
所对的角.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,
, ,
,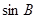 成等差数列,且
成等差数列,且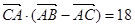 ,求
,求 边的长。
边的长。
已知数列 满足:
满足:
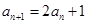 .
.
(Ⅰ)求证:数列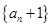 为等比数列;
为等比数列;
(Ⅱ)求数列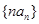 的前
的前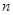 项和
项和 .
.
若以点 为顶点的三角形为直角三角形,求实数
为顶点的三角形为直角三角形,求实数 的值.
的值.
已知函数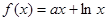 ,其中
,其中 为常数,设
为常数,设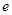 为自然对数的底数.
为自然对数的底数.
(1)若 在区间
在区间 上的最大值为-3,求
上的最大值为-3,求 的值;
的值;
(2)当 时,试推断方程
时,试推断方程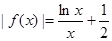 是否有实数解.
是否有实数解.