已知数列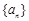 的前n项和
的前n项和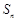 ,满足:
,满足: 三
三
点共线(a为常数,且 ).
).
(Ⅰ)求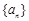 的通项公式;
的通项公式;
(Ⅱ)设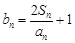 ,若数列
,若数列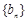 为等比数列,求a的值;
为等比数列,求a的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设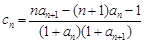 ,数列
,数列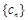 的前n项和为
的前n项和为 ,是否存在最小的整数m,使得任意的n均有
,是否存在最小的整数m,使得任意的n均有 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)如图,在三棱柱 中,
中, 底面
底面 ,
, ,E、F分别是棱
,E、F分别是棱 的中点.
的中点.
(Ⅰ)求证:AB⊥平面AA1 C1C;
(Ⅱ)若线段 上的点
上的点 满足平面
满足平面 //平面
//平面 ,试确定点
,试确定点 的位置,并说明理由;
的位置,并说明理由;
已知向量 .记
.记
(I)求 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(Ⅱ)在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 若
若 ,
, ,
, ,求
,求 的值.
的值.
已知椭圆
 的两个焦点分别为
的两个焦点分别为 ,
, ,离心率为
,离心率为 ,过
,过 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 的周长为
的周长为 .
.
(I)求椭圆 的方程;
的方程;
(Ⅱ)过原点 的两条互相垂直的射线与椭圆
的两条互相垂直的射线与椭圆 分别交于
分别交于 ,
, 两点,求证:点
两点,求证:点 到直线
到直线 的距离为定值,并求出这个定值.
的距离为定值,并求出这个定值.
已知椭圆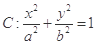
 的两个焦点分别为
的两个焦点分别为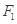 ,
,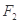 ,离心率为
,离心率为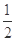 ,过
,过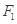 的直线
的直线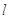 与椭圆
与椭圆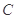 交于
交于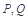 两点,且
两点,且 的周长为
的周长为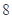 .
.
(1)求椭圆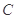 的方程;
的方程;
(2)斜率为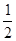 的直线
的直线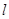 与曲线
与曲线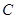 交于
交于 两个不同点,若直线
两个不同点,若直线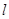 不过点
不过点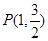 ,设直线
,设直线 的斜率分别为
的斜率分别为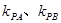 ,求
,求 的数值;
的数值;
(3)试问:是否存在一个定圆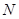 ,与以动点
,与以动点 为圆心,以
为圆心,以 为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.
为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.
(本小题满分13分)已知函数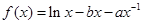 (
(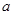 、
、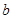 为常数),在
为常数),在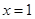 时取得极值
时取得极值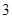 .
.
(I)求实数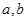 的值;
的值;
(II)求函数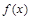 的最小值;
的最小值;
(III)当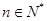 时,试比较
时,试比较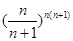 与
与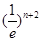 的大小并证明.
的大小并证明.