某组织对男女青年是否喜爱古典音乐进行了一个调查,调查者随机调查了 名青年,下表给出了调查结
名青年,下表给出了调查结
果(单位:人)
(1)用分层抽样的方法在不喜爱古典音乐的青年中抽 人,其中男青年应抽几人?
人,其中男青年应抽几人?
(2)男女青年喜爱古典音乐的程度是否有差异?
(1)解不等式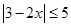 ;
;
(2)已知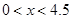 ,求
,求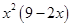 的最大值.
的最大值.
(选修4-5:不等式选讲)设函数 .
.
(1)解不等式 ;
;
(2)若对任意实数 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
(选修4-4:坐标系与参数方程)
在直角坐标系 中,圆
中,圆 的方程为
的方程为 .以
.以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)射线
 与圆
与圆 的交点为
的交点为 、
、 两点,求
两点,求 点的极坐标.
点的极坐标.
已知函数 (
( ).
).
(1)当 时,求
时,求 在
在 的最小值;
的最小值;
(2)若 存在单调递减区间,求
存在单调递减区间,求 的取值范围.
的取值范围.