已知函数f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),其中x∈[0,15],a>0,且a≠1.
(1)若1是关于x的方程f(x)-g(x)=0的一个解,求t的值;
(2)当0<a<1时,不等式f(x)≥g(x)恒成立,求t的取值范围;
已知 ,若
,若 的充分不必要条件,求实数
的充分不必要条件,求实数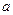 的取值范围。
的取值范围。
画出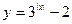 的图象,并利用图象回答:实数
的图象,并利用图象回答:实数 为何值时,方程
为何值时,方程 无解?有一解?有两解?
无解?有一解?有两解?
(本小题满分12分)
已知数列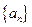 中,
中, (
( 为常数),
为常数),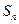 为
为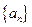 的前
的前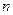 项和,且
项和,且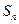 是
是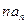 与
与 的等差中项.
的等差中项.
(Ⅰ)求
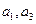 ;
;
(Ⅱ)求数列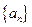 的通项公式;
的通项公式;
(Ⅲ)若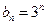 且
且 ,
,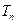 为数列
为数列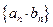 的前
的前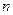 项和,求
项和,求 的值.
的值.
(本小题满分12分)
在数列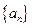 中,已知
中,已知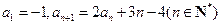
(Ⅰ)求证:数列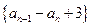 是等比数列;
是等比数列;
(Ⅱ)求数列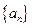 的通项公式;
的通项公式;
(Ⅲ)求数列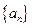 的前
的前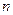 项和
项和
(本小题满分12分)
用黄、蓝、白三种颜色粉刷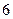 间办公室
间办公室
(Ⅰ)若每间办公室刷什么颜色不要求,有多少种不同的粉刷方法?
(Ⅱ)若一种颜色粉刷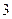 间,一种颜色粉刷
间,一种颜色粉刷 间,一种颜色粉刷
间,一种颜色粉刷 间,有多少种不同的粉刷方法?
间,有多少种不同的粉刷方法?
(Ⅲ)若每种颜色至少用一次,粉刷这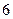 间办公室,有多少种不同的粉刷方法?
间办公室,有多少种不同的粉刷方法?