已知:关于 的一元二次方程
的一元二次方程

(1) 若方程有两个不相等的实数根,求 的取值范围;
的取值范围;
(2)求证:无论 为何值,方程总有一个固定的根;
为何值,方程总有一个固定的根;
(3)若 为整数,且方程的两个根均为正整数,求
为整数,且方程的两个根均为正整数,求 的值.
的值.
以四边形 的边 为斜边分别向外侧作等腰直角三角形,直角顶点分别为 ,顺次连接这四个点,得四边形 .
(1)如图①,当四边形 为正方形时,我们发现四边形 是正方形;
如图②,当四边形 为矩形时,请判断:四边形 的形状(不要求证明);
(2)如图③,当四边形 为一般平行四边形时,设 .
①试用含 的代数式表示 ;
②求证: ;
③四边形 是什么四边形?并说明理由.

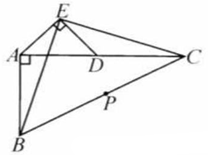
如图,设 为等腰直角三角形 斜边 上任意一点, 于点 于点 于 点, 交 于点 ,延长 并在其延长线上取一点 ,使得 .求证: ,且 .

在 中, ,点 分别是 , 的中点, 是等腰三角形, ,连接 .
(1)判断线段 和 的关系,并证明你的结论;
(2)连接 ,过点 作 ,过点 作 和 相交于点 ,在图中先补充图形,再判断四边形 的形状,并证明你的结论.
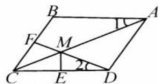
已知,如图,在菱形 中, 为边 的中点, 与对角线 交于点 ,过 作 于点 .
(1)若 ,求 的长;
(2)求证: .
现有一张矩形纸片 (如图)。其中 ,点 是 的中点,将纸片沿直线 折叠,点 落在四边形 内,记为点 ,求线段 的长.
