(本小题满分12分)
为了评估天气对大运会的影响,制定相应预案,深圳市气象局通过对最近50多年的气象数据资料的统计分析,发现8月份是本市雷电天气高峰期,在31天中平均发生雷电14.57天如图 .如果用频率作为概率的估计值,并假定每一天发生雷电的概率均相等,且相互独立.
.如果用频率作为概率的估计值,并假定每一天发生雷电的概率均相等,且相互独立.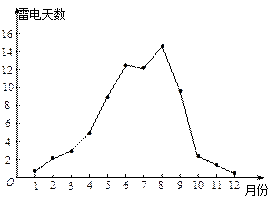
(1)求在大运会开幕(8月12日)后的前3天比赛中,恰好有2天发生雷电天气的概率(精确到0.01);
(2)设大运会期间(8月12日至23日,共12天),发生雷电天气的天数为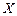 ,求
,求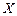 的数学期望和方差.
的数学期望和方差.
已知双曲线的中心在原点,焦点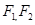 在坐标轴上,离心率为
在坐标轴上,离心率为 ,且过点
,且过点
(1)求双曲线的方程.
(2)若点
(3)在(2)的条件下
求满足下列条件的曲线方程
(1)经过两点P( ,1),Q(
,1),Q(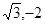 )的椭圆的标准方程.
)的椭圆的标准方程.
(2)与双曲线 有共同的渐近线,且经过点
有共同的渐近线,且经过点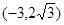 的双曲线的标准方程.
的双曲线的标准方程.
(3)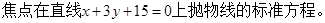
设函数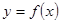 定义在
定义在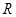 上,对于任意实数
上,对于任意实数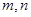 ,恒有
,恒有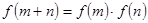 ,且当
,且当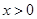 时,
时,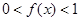
(1)求证: 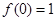 且当
且当 时,
时,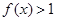
(2)求证: 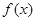 在
在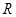 上是减函数;
上是减函数;
(3)设集合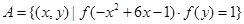 ,
,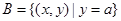 ,且
,且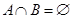 ,
,
求实数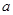 的取值范围。
的取值范围。
某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数: ,其中
,其中 是仪器的月产量。
是仪器的月产量。
(1)将利润 元表示为月产量
元表示为月产量 台的函数;
台的函数;
(2)当月产量为何值时,公司所获得利润最大?最大利润是多少?(总收益=总成本+利润).
已知函数 .
.
(1)证明:不论 为何实数
为何实数 总为增函数
总为增函数
(2)确定 的值, 使
的值, 使 为奇函数;
为奇函数;
(3)当 为奇函数时, 求
为奇函数时, 求 的值域.
的值域.