.已知数列 满足
满足 ,且
,且 。
。
(1)求 ,
,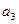 ,
,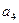 的值;
的值;
(2)猜想数列 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。
(本题满分12分) 已知函数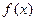 =
=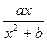 ,在x=1处取得极值为2.(1)求函数
,在x=1处取得极值为2.(1)求函数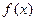 的解析式;(2)若函数
的解析式;(2)若函数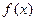 在区间(m,2m+1)上为增函数,求实数m的取值范围;(3)若P(x0,y0)为
在区间(m,2m+1)上为增函数,求实数m的取值范围;(3)若P(x0,y0)为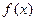 =
=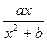 图象上的任意一点,直线l与
图象上的任意一点,直线l与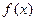 =
=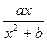 的图象相切于点P,求直线l的斜率的取值范围.
的图象相切于点P,求直线l的斜率的取值范围.
(本小题满分14分)
设函数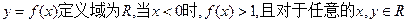 ,有
,有 。
。
(1)求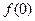 的值;(2)求数列
的值;(2)求数列 的通项公式;(3)是否存在正数
的通项公式;(3)是否存在正数 均成立,若存在,求出k的最大值,并证明,否则说明理由。
均成立,若存在,求出k的最大值,并证明,否则说明理由。
(本小题满分12分)


|
|
如图,A为椭圆 上
上
|
|
 的一个动点,弦AB、AC分别过焦点
的一个动点,弦AB、AC分别过焦点
|
F1、F2。当AC垂直于x轴时,恰好
|
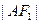 ∶
∶ =3∶1.
=3∶1.
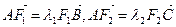 ,试判断
,试判断 是否为定值?若是,则求出该定值;若不是,请说明理由。
是否为定值?若是,则求出该定值;若不是,请说明理由。
(本小题满分12分)在正方体 中,棱长
中,棱长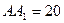 .
.
(1)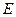 为棱
为棱 的中点,求证:
的中点,求证: ;
;
(2)求二面角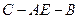 的大小;
的大小;
(3)求点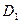 到平面
到平面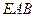 的距离.
的距离.
(本小题满分12分)已知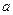 为实数,函数
为实数,函数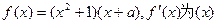 的导函数。(1)若
的导函数。(1)若 上的最大值和最小值;(2)若函数
上的最大值和最小值;(2)若函数 有两个不同的极值点,求
有两个不同的极值点,求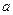 的取值范围。
的取值范围。