本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分
某厂生产某种零件,每个零件的成本为50元,出厂单价定为80元,该厂为鼓励销售商订购,决 定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.04元,但实际出厂单价最低不能低于60元。
定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.04元,但实际出厂单价最低不能低于60元。
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为60元?
(2)设一次订购量为 个,零件的实际出厂单价为P元,写出函数P=
个,零件的实际出厂单价为P元,写出函数P= 的表达式;
的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
椭圆C: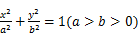 的离心率为
的离心率为 ,P(m,0)为C的长轴上的一个动点,过P点斜率为
,P(m,0)为C的长轴上的一个动点,过P点斜率为 的直线l交C于A、B两点.当m=0时,
的直线l交C于A、B两点.当m=0时,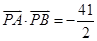 .
.
(1)求C的方程;
(2)证明: 为定值.
为定值.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(1)求证:平面BCE⊥平面CDE;
(2)求二面角B-EF-D的余弦值.
设函数 .
.
(1)若方程f(x)=3x在(1,2)上有根,求a的取值范围;
(2)设 ,若对任意的
,若对任意的 ,都有
,都有 ,求a的取值范围
,求a的取值范围
设函数 直线
直线
 与函数f(x)图像相邻两交点的距离为
与函数f(x)图像相邻两交点的距离为 .
.
(1)求 的值;
的值;
(2)若g(x)=af(x)+b在 上的最大值为
上的最大值为 ,最小值为1,求a+b的值.
,最小值为1,求a+b的值.
设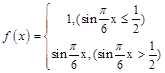 ,g(x)=|x|+|6-x|,令F(x)=f(x)+g(x),若关于a的方程
,g(x)=|x|+|6-x|,令F(x)=f(x)+g(x),若关于a的方程 有且仅有四个不等实根,则m的取值范围为.
有且仅有四个不等实根,则m的取值范围为.