(本小题满分12分)品厂为了检查甲、乙两条自动包装流水线的生产情况,在这两条
流水线上各抽取40件产品作为样本称 出它们的重量(单位:克),重量值落在(495,510]
出它们的重量(单位:克),重量值落在(495,510]
的产 品为合格品,否则为不合格品,表1是甲流水线样本频数分布表,
品为合格品,否则为不合格品,表1是甲流水线样本频数分布表, 图1是乙流水线样
图1是乙流水线样
本的频率分布直方图。 某食
某食
(1)若检验员不小心将甲、乙两条流水线生产的重量值在(510,515]的产品放在了一起,
然后又随机取出3件产品,求至少有一件是乙流水线生产的产品的概率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。
| |
甲流水线 |
乙流水线 |
合 计 |
| 合格品 |
a= |
b= |
|
| 不合格品 |
c= |
d= |
|
| 合 计 |
|
|
n= |
在直角坐标系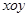 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点
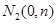 ,且
,且 .
.
(Ⅰ)求直线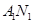 与
与 交点的轨迹
交点的轨迹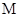 的方程;
的方程;
(Ⅱ)已知点 (
( )是轨迹
)是轨迹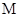 上的定点,
上的定点,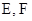 是轨迹
是轨迹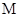 上的两个动点,如果直线
上的两个动点,如果直线 的斜率
的斜率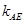 与直线
与直线 的斜率
的斜率 满足
满足 ,试探究直线
,试探究直线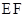 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
如图,已知△AOB,∠AOB= ,∠BAO=
,∠BAO= ,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为
,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为 .
.
(Ⅰ)当平面COD⊥平面AOB时,求 的值;
的值;
(Ⅱ)当 ∈[
∈[ ,
, ]时,求二面角C-OD-B的余弦值的取值范围.
]时,求二面角C-OD-B的余弦值的取值范围.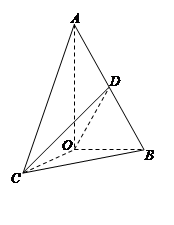
已知数列 满足:
满足:
(Ⅰ)求证:数列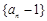 是等比数列;
是等比数列;
(Ⅱ)令 (
(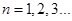 ),如果对任意
),如果对任意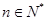 ,都有
,都有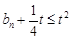 ,
,
求实数 的取值范围.
的取值范围.
已知点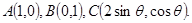
(Ⅰ)若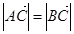 ,求
,求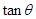 的值;
的值;
(Ⅱ)若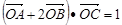 ,其中
,其中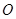 为坐标原点,求
为坐标原点,求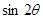 的值
的值
如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,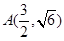 是曲线C1和C2的交点.
是曲线C1和C2的交点.
(Ⅰ)求曲线C1和C2所在的椭圆和抛物线的方程;
(Ⅱ)过F2作一条与x轴不垂直的直线,分别与曲线C1、C2依次交于B、C、D、E四点,若G为CD中点,H为BE中点,问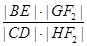 是否为定值,若是,求出定值;若不是,请说明理由.
是否为定值,若是,求出定值;若不是,请说明理由.