(本小题满分 14分)已知数列
14分)已知数列 是以
是以 d为公差的等差数列,数列
d为公差的等差数列,数列 是以q为公比的
是以q为公比的
等比数列。
(1)若数列 的前n项和为
的前n项和为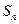 且
且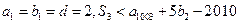 ,求整数q的值;
,求整数q的值;
(2)在(1)的条件下,试问数列 中最否存在一项
中最否存在一项 ,使得
,使得 恰好可以表示为该数列
恰好可以表示为该数列
中连续 项的和?请说明理由;
项的和?请说明理由;
(3)若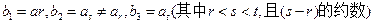 ,求证:数列
,求证:数列
中每一项都是数列 中的项。
中的项。
已知等差数列{an}的前n项中a1是最小的,且a1+a4=6,a2·a3=5,Sn=150,求n的值。
已知向量m=(cosθ,sinθ)和n=(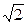 -sinθ,cosθ),θ∈[π,2π].
-sinθ,cosθ),θ∈[π,2π].
(1)求|m+n|的最大值;
(2)当|m+n|= 时,求cos(
时,求cos(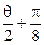 )的值.
)的值.
(本小题满分12分)标准椭圆 的两焦点为
的两焦点为 ,
, 在椭圆上,且
在椭圆上,且 .(1)求椭圆方程;(2)若N在椭圆上,O为原点,直线
.(1)求椭圆方程;(2)若N在椭圆上,O为原点,直线 的方向向量为
的方向向量为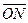 ,若
,若 交椭圆于A、B两点,且NA、NB与
交椭圆于A、B两点,且NA、NB与 轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
(本小题满分12分)已知函数 ,且函数
,且函数 的图象关于原点对称,其图象在
的图象关于原点对称,其图象在 处的切线方程为
处的切线方程为 (1)求
(1)求 的解析式;(2)是否存在区间
的解析式;(2)是否存在区间 使得函数
使得函数 的定义域和值域均为
的定义域和值域均为 ,且其解析式为f(x)的解析式?若存在,求出这样的一个区间[m,n];若不存在,则说明理由.
,且其解析式为f(x)的解析式?若存在,求出这样的一个区间[m,n];若不存在,则说明理由.
(本小题满分12分)已知ABCD是矩形, ,E、F分别是线段AB、BC的中点,
,E、F分别是线段AB、BC的中点, 面ABCD.(1)
面ABCD.(1) 证明:PF⊥FD;
证明:PF⊥FD;
(2)在PA上找一点G,使得EG∥平面PFD.