(本小题满分12分)标准椭圆 的两焦点为
的两焦点为 ,
, 在椭圆上,且
在椭圆上,且 . (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线
. (1)求椭圆方程;(2)若N在椭圆上,O为原点,直线 的方向向量为
的方向向量为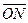 ,若
,若 交椭圆于A、B两点,且NA、NB与
交椭圆于A、B两点,且NA、NB与 轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
如图所示的多面体是由底面为 的长方体被截面
的长方体被截面 所截面而得到的,其中
所截面而得到的,其中 ,
, .
.
(Ⅰ)求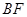 的长;
的长;
(Ⅱ)求点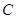 到平面
到平面 的距离.
的距离.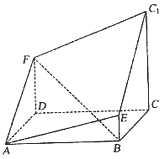
数列{ }满足
}满足
(1)若{ }是等差数列,求其通项公式;
}是等差数列,求其通项公式;
(2)若{ }满足
}满足 为{
为{ }的前
}的前 项和,求
项和,求 .
.
已知函数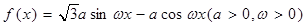 的图象上两相邻最高点的坐标分别为
的图象上两相邻最高点的坐标分别为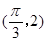 和
和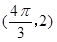
(1)求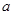 与
与 的值;
的值;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,且f (A )=2,求 的值.
的值.
经市场调查,某种商品在120天内的日销售量和售价均为时间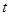 (天)的函数,日销售量与时间的关系用图(1)的一条折线表示,售价与时间的关系用图(2)的一条折线表示。
(天)的函数,日销售量与时间的关系用图(1)的一条折线表示,售价与时间的关系用图(2)的一条折线表示。
(Ⅰ)写出图(1)表示的日销售量(千克)与时间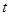 的函数关系史
的函数关系史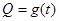 ;
;
写出图(2)表示的售价(元 /千克)与时间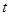 的函数关系式
的函数关系式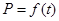 ;
;
(Ⅱ)求日销售额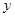 (元)与时间的函数关系式,并求出日销售额最高的是哪一天?最高的销售额是多少?(注:日销售额=日销售量×售价)
(元)与时间的函数关系式,并求出日销售额最高的是哪一天?最高的销售额是多少?(注:日销售额=日销售量×售价)
已知函数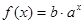 (其中
(其中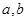 为常量且
为常量且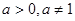 )的图像经过点
)的图像经过点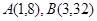 .
.
(Ⅰ)试求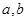 的值;
的值;
(Ⅱ)若不等式 在
在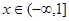 时恒成立,求实数
时恒成立,求实数 的取值范围
的取值范围