选修44:坐标系与参数方程
求曲线C1:被直线l:y=x-所截得的线段长.
(本小题满分12分)已知数列 的前
的前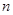 项和为
项和为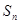 ,且
,且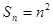
(1)求数列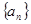 的通项公式;
的通项公式;
(2)记数列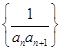 的前
的前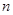 项和为
项和为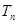 ,若对任意的
,若对任意的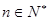 ,
, 恒成立,求实数
恒成立,求实数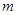 的取值范围.
的取值范围.
已知
(1)证明:
(2)若 在
在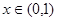 恒成立,求
恒成立,求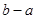 的最小值.
的最小值.
(3)证明: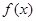 图像恒在直线
图像恒在直线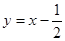 的上方.
的上方.
(本题满分14分) 己知函数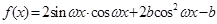 (其中
(其中 )的最大值为
)的最大值为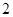 ,直线
,直线 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且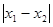 的最小值为
的最小值为 .
.
(1)求函数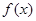 的单调增区间;
的单调增区间;
(2)若 ,求
,求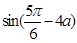 的值;
的值;
(3)对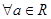 ,在区间
,在区间 上
上 有且只有
有且只有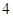 个零点,请直接写出满足条件的所有
个零点,请直接写出满足条件的所有 的值并把上述结论推广到一般情况.(不要求证明)
的值并把上述结论推广到一般情况.(不要求证明)
中国正在成为汽车生产大国,汽车保有量大增,交通拥堵日趋严重.某市有关部门进行了调研,相关数据显示,从上午 点到中午
点到中午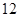 点,车辆通过该市某一路段的用时
点,车辆通过该市某一路段的用时 (分钟)与车辆进入该路段的时刻
(分钟)与车辆进入该路段的时刻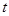 之间关系可近似地用如下函数给出:
之间关系可近似地用如下函数给出: ,
,
求从上午 点到中午
点到中午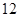 点,车辆通过该路段用时最多的时刻.
点,车辆通过该路段用时最多的时刻.
在 中,
中, 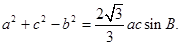
(1)求 的大小;
的大小;
(2)若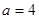 ,且
,且 ,求边
,求边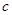 的取值范围.
的取值范围.