(本题满分14分) 己知函数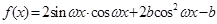 (其中
(其中 )的最大值为
)的最大值为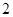 ,直线
,直线 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且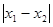 的最小值为
的最小值为 .
.
(1)求函数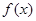 的单调增区间;
的单调增区间;
(2)若 ,求
,求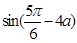 的值;
的值;
(3)对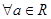 ,在区间
,在区间 上
上 有且只有
有且只有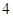 个零点,请直接写出满足条件的所有
个零点,请直接写出满足条件的所有 的值并把上述结论推广到一般情况.(不要求证明)
的值并把上述结论推广到一般情况.(不要求证明)
若关于x的方程3x2-5x+a=0的一个根在(-2,0)内,另一个根在(1,3)内,求a的取值范围.
已知函数y=f(x)是定义在区间[-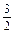 ,
,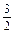 ]上的偶函数,且x∈[0,
]上的偶函数,且x∈[0,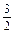 ]时,f(x)=-x2-x+5.(1)求函数f(x)的解析式;
]时,f(x)=-x2-x+5.(1)求函数f(x)的解析式;
(2)若矩形ABCD的顶点A,B在函数y=f(x)的图象上,顶点C,D在x轴上,求矩形ABCD面积的最大值.
设a,b∈R,且a≠2,定义在区间(-b,b)内的函数f(x)=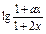 是奇函数.
是奇函数.
(1)求b的取值范围;
(2)讨论函数f(x)的单调性.
等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S.
(1)求函数S=f(x)的解析式;
(2)试确定点P的位置,使△ABP的面积S最大.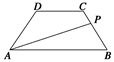
设直线x=1是函数f(x)的图象的一条对称轴,对于任意x∈R,f(x+2)=-f(x),当-1≤x≤1时,f(x)=x3.
(1)证明:f(x)是奇函数;
(2)当x∈[3,7]时,求函数f(x)的解析式.