（本题满分 12 分）本题共有 3 个小题，第 1 小题满分 3分，第 2 小题满分 4分，第 3小题满分5 分．
设数列
的首项
为常数，且
．
（1）证明：
是等比数列；
（2）若
，中是否存在连续三项成等差数列？若存在，写出这三项，若不存在说明理由．
（3）若是递增数列，求的取值范围．
（本题满分 10 分）本题共有 2 个小题，第 1 小题满分 4 分，第 2 小题满分6分．
在平面直角坐标系
中，点
到两点
、
的距离之和等于4．设点的轨迹为
．
（1）写出轨迹的方程；
（2）设直线
与交于
、
两点，问
为何值时
此时|
|的值是多少？
（本题满分 8 分）有根木料长为6米，要做一个如图的窗框，已知上框架与下框架的高的比为1∶2，问怎样利用木料，才能使光线通过的窗框面积最大（中间木档的面积可忽略不计）.
本题共有 3 个小题，第 1 小题满分 3 分，第 2 小题满分4分，第 3 小题满分5分．
已知抛物线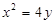
，过原点作斜率为1的直线交抛物线于第一象限内一点
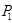，又过点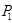作斜率为
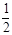的直线交抛物线于点
，再过作斜率为
的直线交抛物线于点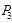
，
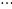，如此继续。一般地，过点
作斜率为
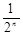的直线交抛物线于点
，设点
．
（1）求
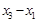的值；
（2）令
，求证：数列
是等比数列；
（3）记
为点列
的极限点，求点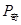
的坐标．
（本题满分 10 分）本题共有 2 个小题，第 1 小题满分 4 分，第 2 小题满分6分．
已知函数
．
（1）写出函数
的奇偶性；
（2）当
时，是否存实数
，使的图像在函数
图像的下方，若存在，求的取值范围；若不存在，说明理由．
的定义域； 
的值域。