甲、乙两人各进行3次射击，甲每次击中目标的概率为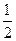
，乙每次击中目标的概率为
.
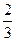（1）记甲击中目标的次数为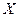
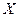，求的概率分布列及数学期望EX；
（2）求甲恰好比乙多击中目标2次的概率.
（本小题满分12分）
已知在
中，角
，
，
的对边的边长分别为
，
，
，且
．
（Ⅰ）求角
的大小；
（Ⅱ）现给出三个条件：①
；②
；③
．
试从中选出两个可以确定的条件，写出你的选择，并以此为依据求出
的面积．（只需写出一个选定方案即可，选多种方案以第一种方案记分）
（本小题满分12分）
已知点Pn(an,bn)都在直线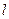
：y=2x+2上，P1为直线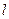与x轴的交点，数列
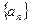成等差数列，公差为1.（n∈N+）
（1）求数列，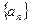
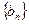的通项公式；
（2）若f(n)=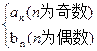
问是否存在k
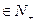,使得f(k+5)=2f(k)－2成立；若存在，求出
k的值，若不存在，说明理由。
（3）求证：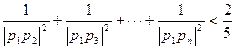
（n≥2，n∈N+）
（本小题满分12分）
已知点(x, y) 在曲线C上，将此点的纵坐标变为原来的2倍,对应的横坐标不变,得到的点满足方程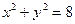
；定点M(2,1)，平行于OM的直线
在y轴上的截距为m(m≠0),直线与曲线C交于A、B两个不同点.
(1)求曲线
的方程；
(2)求m的取值范围.
（（本小题满分12分）
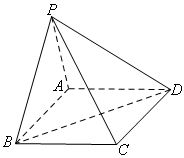
如图，在四棱锥
中，底面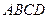
是矩形．已知
．
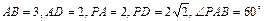（1）证明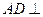
平面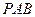
；
（2）求异面直线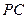
与
所成的角的大小；
（3）求二面角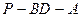
的大小．
（（本小题满分12分）
如图，在棱长为2的正方体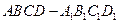
中，
、
分别为
、
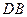的中点．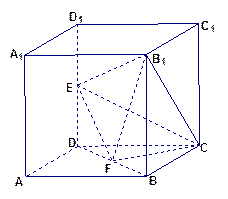
（1）求证：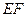
//平面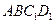
；
（2）求证：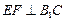
；
（3）求三棱锥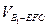
的体积．