(本小题满分14分)
已知函数 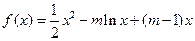 ,
,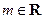 .
.
(Ⅰ)当 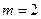 时,求函数
时,求函数 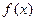 的最小值;
的最小值;
(Ⅱ)当 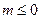 时,讨论函数
时,讨论函数 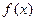 的单调性;
的单调性;
(Ⅲ)求证:当 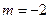 时,对任意的
时,对任意的  ,且
,且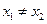 ,有
,有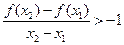 .
.
(本小题满分16分)设函数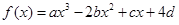 (
(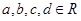 )的图象关于原点对称,且
)的图象关于原点对称,且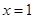 时,
时,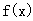 取极小值
取极小值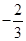 ,
,
①求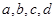 的值;
的值;
②当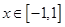 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
③若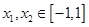 ,求证:
,求证: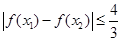 。
。
已知,数列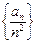
 是公比为
是公比为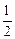 的等比数列,
的等比数列,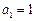 .
.
(1)求数列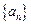 的通项公式;
的通项公式;
(2)令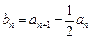 ,若数列
,若数列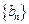 的前
的前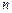 项和
项和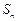 ,求证:
,求证: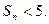
(本小题满分14分)
(理)已知数列{a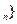 中,a
中,a =5且a
=5且a =3a
=3a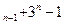 (n≥2)
(n≥2)
(1)求a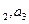 的值.
的值.
(2)设b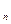 =
=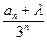 ,是否存在实数λ,使数列{b
,是否存在实数λ,使数列{b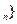 为等差数列,若存在请求其通项b
为等差数列,若存在请求其通项b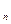 ,若不存在请说明理由.
,若不存在请说明理由.
|
如图,四棱锥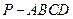 的底面
的底面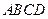 是正方形,侧棱
是正方形,侧棱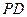 ⊥底面
⊥底面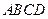 ,
,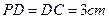 ,
,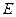 为
为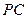 的中点.
的中点.
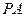 //平面
//平面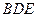 ;
;
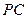 上是否存在点
上是否存在点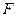 ,使三棱锥
,使三棱锥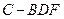 的
的
 积为
积为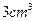 ?并说明理由.
?并说明理由.
现有8名数理化成绩优秀者,其中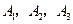 数学成绩优秀,
数学成绩优秀,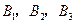 物理成绩优秀,
物理成绩优秀,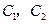 化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛
化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛
(Ⅰ)求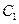 被选中的概率;
被选中的概率;
(Ⅱ)求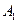 和
和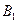 不全被选中的概率
不全被选中的概率