已知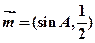
与
共线，其中A是△ABC的内角．
（1）求角A的大小；
（2）若BC=2，求△ABC面积S的最大值，并判断S取得最大值时△ABC的形状.
已知A={x|﹣1＜x＜4}，
，C={x|x＜2a}
求：（1）A∪B
（2）A⊆C求a的取值范围．
化简、求值：
（1）
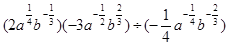
（2）
已知二次函数f（x）=ax2+bx+1（a，b∈R，a＞0），设方程f（x）=x的两个实数根为x1和x2．
（1）如果x1＜2＜x2＜4，设二次函数f（x）的对称轴为x=x0，求证：x0＞﹣1；
（2）如果|x1|＜2，|x2﹣x1|=2，求b的取值范围．
已知函数
．
（1）当a=4，解不等式
；
（2）若不等式f（x）<x在[1，+∞）恒成立，求实数a的取值范围．
某校在一次趣味运动会的颁奖仪式上，高一、高二、高三各代表队人数分别为120人、120人、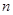
人．为了活跃气氛，大会组委会在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取20人在前排就坐，其中高二代表队有6人．
（1）求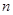的值；
（2）把在前排就坐的高二代表队6人分别记为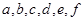
，现随机从中抽取2人上台抽奖，求
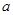和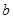
至少有一人上台抽奖的概率；
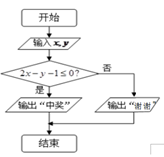
（3）抽奖活动的规则是：代表通过操作按键使电脑自动产生两个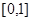
之间的均匀随机数
，并按如右所示的程序框图执行．若电脑显示“中奖”，则该代表中奖；若电脑显示“谢谢”，则不中奖，求该代表中奖的概率．