已知函数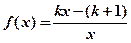
(1)若函数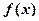 是
是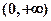 上的增函数,求
上的增函数,求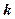 的取值范围;
的取值范围;
(2)证明:当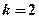 时,不等式
时,不等式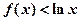 对任意
对任意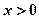 恒成立;
恒成立;
(3)证明: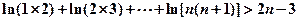
已知点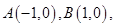 直线AM,BM相交于点M,且
直线AM,BM相交于点M,且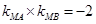 .
.
(1)求点M的轨迹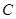 的方程;
的方程;
(2)过定点(0,1)作直线PQ与曲线C交于P,Q两点,且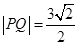 ,求直线PQ的方程.
,求直线PQ的方程.
已知数列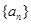 满足
满足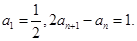
(1)求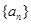 的通项公式;
的通项公式;
(2)证明: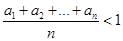 .
.
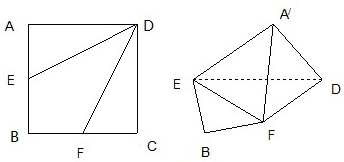
如图,边长为2的正方形ABCD,E,F分别是AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于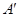 .
.
(1)求证: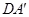 ⊥EF;
⊥EF;
(2)求二面角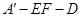 的平面角的余弦值.
的平面角的余弦值.
在一个盒子里装有6枝圆珠笔,其中3枝一等品,2枝二等品,1枝三等品.
(1)从盒子里任取3枝恰有1枝三等品的概率多大?;
(2)从盒子里任取3枝,设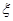 为取出的3枝里一等品的枝数,求
为取出的3枝里一等品的枝数,求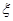 的分布列及数学期望.
的分布列及数学期望.
已知函数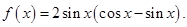
(1)当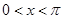 时,求
时,求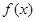 的最大值及相应的x值;
的最大值及相应的x值;
(2)利用函数y=sin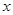 的图象经过怎样的变换得到f(x)的图象.
的图象经过怎样的变换得到f(x)的图象.