(本小题满分12分)设同时满足条件:①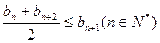 ;②
;②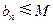 (
(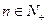 ,
, 是与
是与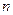 无关的常数)的无穷数列
无关的常数)的无穷数列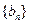 叫“特界”数列.
叫“特界”数列.
(1)若数列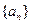 为等差数列,
为等差数列,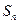 是其前
是其前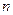 项和,
项和,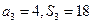 ,求
,求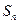 ;
;
(2)判断(1)中的数列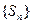 是否为“特界” 数列,并说明理由。
是否为“特界” 数列,并说明理由。
已知数列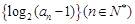 为等差数列,且
为等差数列,且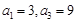 .
.
(1)求数列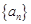 的通项公式;
的通项公式;
(2)证明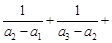 …
…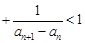 .
.
已知函数 .
.
(1)当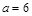 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若函数 有两个极值点
有两个极值点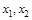 ,且
,且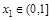 ,求证:
,求证: ;
;
(Ⅲ)设 ,对于任意
,对于任意 时,总存在
时,总存在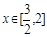 ,使
,使 成立,求实数
成立,求实数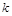 的取值范围.
的取值范围.
已知抛物线C: ,定点M(0,5),直线
,定点M(0,5),直线 与
与 轴交于点F,O为原点,若以OM为直径的圆恰好过
轴交于点F,O为原点,若以OM为直径的圆恰好过 与抛物线C的交点.
与抛物线C的交点.
(1)求抛物线C的方程;
(2)过点M作直线交抛物线C于A,B两点,连AF,BF延长交抛物线分别于 ,求证: 抛物线C分别过
,求证: 抛物线C分别过 两点的切线的交点Q在一条定直线上运动.
两点的切线的交点Q在一条定直线上运动.
已知正项数列{an}中,a1=1,且log3an,log3an+1是方程x2 (2n
(2n 1)x+bn=0的两个实根.
1)x+bn=0的两个实根.
(1)求a2,b1;
(2)求数列{an}的通项公式;
(3)若 ,
, 是
是 前
前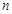 项和,
项和,  ,当
,当 时,试比较
时,试比较 与
与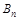 的大小.
的大小.
已知平行四边形ABCD(图1)中,AB=4,BC=5,对角线AC=3,将三角形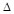 ACD沿AC折起至
ACD沿AC折起至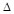 PAC位置(图2),使二面角
PAC位置(图2),使二面角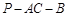 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.
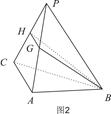
(1)求证:PC 平面BGH;
平面BGH;
(2)求平面PAB与平面BGH夹角的余弦值.