(本小题满分14分)在平面直角坐标系 中,已知椭圆
中,已知椭圆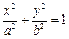 (
( )的离心率为
)的离心率为 ,其焦点在圆
,其焦点在圆 上.
上.
(1)求椭圆的方程;
(2)设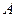 、
、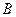 、
、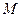 是椭圆上的三点(异于椭圆顶点),且存在锐角
是椭圆上的三点(异于椭圆顶点),且存在锐角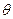 ,使
,使 .
.
(i)求证:直线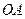 与
与 的斜率之积为定值;
的斜率之积为定值;
(ii)求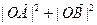 .
.
已知函数 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1.
(1)求实数a的值,并求函数 的单调区间,
的单调区间,
(2)若不等式 ≥k在区间
≥k在区间 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其
范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.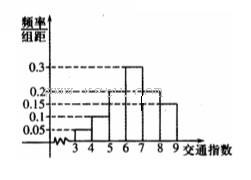
(1)请补全直方图,并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个?
(2)用分层抽样的方法从交通指数在[4,6),[6,8),[8,l0]的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽出的6个路段中任取2个,求至少一个路段为轻度拥堵的概率.
如图,在几何体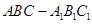 中,点
中,点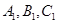 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且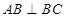 ,E为
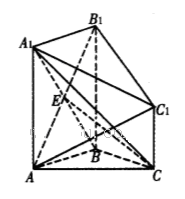
,E为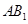 中点,
中点,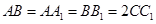 .
.
(1)求证;CE∥平面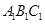 ,
,
(2)求证:平面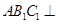 平面
平面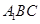
数列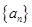 的前n项和为
的前n项和为 ,且
,且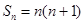 ,数列
,数列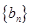 满足
满足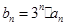 .
.
(1)求数列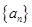 的通项公式,
的通项公式,
(2)求数列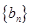 的前n项和.
的前n项和.
已知向量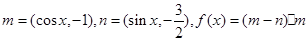 .
.
(1)求函数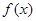 的单调增区间;
的单调增区间;
(2)已知锐角△ABC中角A,B,C的对边分别为a,b,c.其面积 ,
,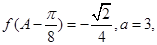 求b+c的值.
求b+c的值.