(本小题满分13分)已知函数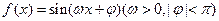 的部分图象如题(18)图所示.
的部分图象如题(18)图所示.
(I)求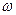 ,
, 的值;
的值;
(II)设 ,求
,求 的单调递增区间.
的单调递增区间.
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 .①证明:平面
.①证明:平面 平面
平面 ; ②若二面角
; ②若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
从集合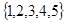 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个.
①记性质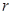 :集合中的所有元素之和为10,求所取出的非空子集满足性质
:集合中的所有元素之和为10,求所取出的非空子集满足性质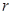 的概率;
的概率;
②记所取出的非空子集的元素个数为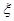 ,求
,求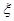 的分布列和数学期望
的分布列和数学期望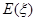 .
.
在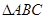 中,角
中,角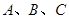 的对边分别为
的对边分别为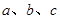 ,且
,且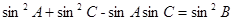 .
.
①求角 的大小;
的大小;
②求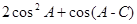 的取值范围.
的取值范围.
已知椭圆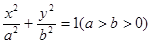 的右焦点为
的右焦点为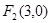 ,离心率为
,离心率为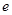 .
.
(1)若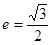 ,求椭圆的方程; (2)设直线
,求椭圆的方程; (2)设直线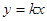 与椭圆相交于
与椭圆相交于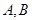 两点,
两点,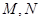 分别为线段
分别为线段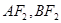 的中点.若坐标原点
的中点.若坐标原点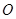 在以
在以 为直径的圆上,且
为直径的圆上,且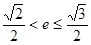 ,求
,求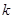 的取值范围.
的取值范围.
已知抛物线C: ,
,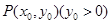 为抛物线上一点,
为抛物线上一点, 为
为 关于
关于 轴对称的点,
轴对称的点, 为坐标原点.(1)若
为坐标原点.(1)若 ,求
,求 点的坐标;
点的坐标;
(2)若过满足(1)中的点 作直线
作直线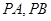 交抛物线
交抛物线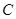 于
于 两点, 且斜率分别为
两点, 且斜率分别为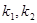 ,且
,且 ,求证:直线
,求证:直线 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.