(本小题满分10分)(注意:在试题卷上作答无效)
在ΔABC中,角A、B、C的对边分别为 ,且满足
,且满足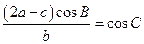 ,
,
(I )求角B的大小;
(II)设 ,且
,且 的最大值是5,求k的值
的最大值是5,求k的值
(文科)已知椭圆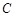 :
: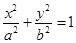
 离心率为
离心率为 ,且椭圆的长轴比焦距长
,且椭圆的长轴比焦距长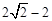 .
.
(1)求椭圆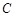 的方程;
的方程;
(2)过点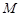 (
( ,
,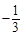 )的动直线
)的动直线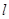 交椭圆
交椭圆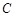 于
于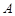 、
、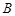 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得无论
,使得无论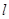 如何转动,以
如何转动,以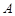
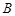 为直径的圆恒过定点
为直径的圆恒过定点 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(文科)已知点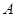 是椭圆
是椭圆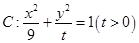 的左顶点,直线
的左顶点,直线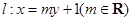 与椭圆
与椭圆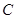 相交于
相交于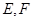 两点,与
两点,与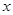 轴相交于点
轴相交于点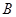 .且当
.且当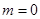 时,△
时,△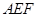 的面积为
的面积为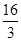 .
.
(Ⅰ)求椭圆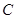 的方程;
的方程;
(Ⅱ)设直线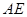 ,
,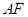 与直线
与直线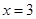 分别交于
分别交于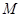 ,
,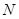 两点,试判断以
两点,试判断以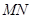 为直径的圆是否经过点
为直径的圆是否经过点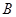 ?并请说明理由.
?并请说明理由.
(文科)已知抛物线P:x2="2py" (p>0).
(Ⅰ)若抛物线上点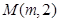 到焦点F的距离为
到焦点F的距离为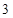 .
.
(ⅰ)求抛物线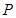 的方程;
的方程;
(ⅱ)设抛物线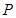 的准线与y轴的交点为E,过E作抛物线
的准线与y轴的交点为E,过E作抛物线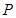 的切线,求此切线方程;
的切线,求此切线方程;
(Ⅱ)设过焦点F的动直线l交抛物线于A,B两点,连接 ,
,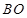 并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
(理科)已知椭圆的焦点坐标为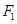 (-1,0),
(-1,0),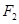 (1,0),过
(1,0),过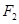 垂直于长轴的直线交椭圆于P、Q两点,且|PQ|=3,
垂直于长轴的直线交椭圆于P、Q两点,且|PQ|=3,
(1)求椭圆的方程;
(2)过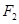 的直线l与椭圆交于不同的两点M、N,则△
的直线l与椭圆交于不同的两点M、N,则△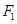 MN的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
MN的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
(文科)已知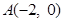 ,
,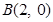 为椭圆
为椭圆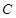 的左、右顶点,
的左、右顶点,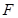 为其右焦点,
为其右焦点,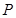 是椭圆
是椭圆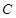 上异于
上异于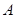 ,
,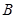 的动点,且
的动点,且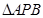 面积的最大值为
面积的最大值为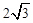 .
.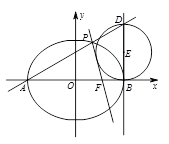
(Ⅰ)求椭圆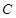 的方程及离心率;
的方程及离心率;
(Ⅱ)直线 与椭圆在点
与椭圆在点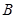 处的切线交于点
处的切线交于点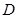 ,当直线
,当直线 绕点
绕点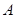 转动时,试判断以
转动时,试判断以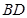 为直径的圆与直线
为直径的圆与直线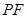 的位置关系,并加以证明.
的位置关系,并加以证明.