(本小题满分12分)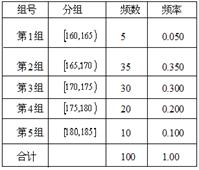
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
(I)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(II)在(I)的前提下,学校决定在这6名学生中,随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?
(本小题满分14分)
在等比数列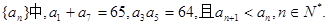
(1)求数列{an}的通项公式;
(2)求数列{an}的前5项的和 ;
;
(3)若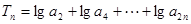 ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值.
(本小题满分12分)
己知数列 中,
中, ,
, ,
,
(1)求证:数列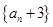 是等比数列;
是等比数列;
(2)若 ,
,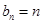 ,求数列
,求数列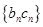 的前
的前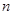 项和
项和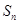 .
.
(本小题满分12分)
一缉私艇A发现在北偏东 方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南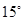 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东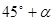 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和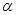 角的正弦值.
角的正弦值.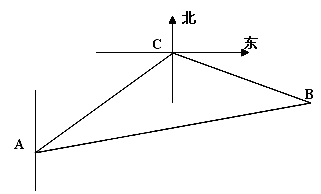
(本小题满分12分)
在 中,
中,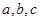 分别是角A、B、C的对边,且
分别是角A、B、C的对边,且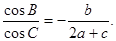
(1)求角B的大小;
(2)若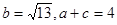 ,求
,求 的面积.
的面积.
已知数列{an}的前n项和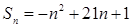 ,
,
(1)求数列{an}的通项公式;
(2)求前n项和 的最大值,并求出相应的
的最大值,并求出相应的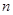 的值.
的值.