(本小题满分14分)
已知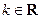 函数
函数 .
.
(I) 若 且函数
且函数 为奇函数,求实数
为奇函数,求实数 ;
;
(II) 若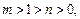 试判断函数
试判断函数 的单调性;
的单调性;
(III) 当 ,
, ,
, 时,求函数
时,求函数 的对称轴或对称中心.
的对称轴或对称中心.
设三组实验数据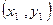 .
.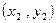 .
.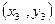 的回归直线方程是:
的回归直线方程是: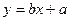 ,使代数式
,使代数式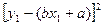
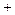
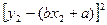
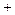
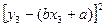 的值最小时,
的值最小时,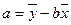 ,
,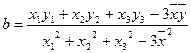 ,(
,(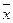 、
、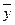 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)
若有七组数据列表如下:
| x |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| y |
4 |
6 |
5 |
6.2 |
8 |
7.1 |
8.6 |
(Ⅰ)求上表中前三组数据的回归直线方程;
(Ⅱ)若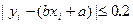 ,即称
,即称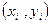 为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, , 且
, 且 .\
.\
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)设 ,且
,且 的最小正周期为
的最小正周期为 ,求
,求 在
在 上的最大值.
上的最大值.
(本小题满分12分)
已知函数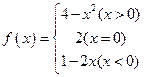 ,
,
(1)画出函数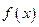 图像;
图像;
(2)求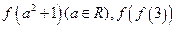 的值;
的值;
(3)当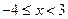 时,求
时,求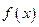 取值的集合.
取值的集合.
(本小题满分12分)
已知定义在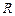 上的函数
上的函数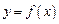 是偶函数,且
是偶函数,且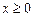 时,
时, ,(1)当
,(1)当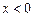 时,求
时,求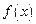 解析式;(2)写出
解析式;(2)写出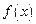 的单调递增区间
的单调递增区间
(1)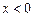 时,
时,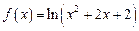
(2)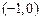 和
和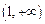
(本小题满分12分)
试讨论函数f(x)=loga (a>0且a≠1)在(1,+∞)上的单调性,并予以证明.
(a>0且a≠1)在(1,+∞)上的单调性,并予以证明.