设直线l与抛物线y2=2px（p>0）交于A、B两点，已知当直线l经过抛物线的焦点且与x轴垂直时，△OAB的面积为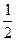
（O为坐标原点）．
（Ⅰ）求抛物线的方程；
（Ⅱ）当直线l经过点P（a，0）（a>0）且与x
轴不垂直时，
若在x轴上存在
点C，使得△ABC为等边三角形，求a
的取值范围．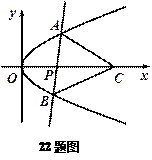
椭圆＋＝1(a>b>0)的一个顶点为A(0,2)，离心率e＝.
(1)求椭圆的方程；
(2)直线l：y＝kx－2(k≠0)与椭圆相交于不同的两点M、N，且满足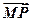
＝
，
·
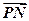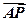＝0，求直线l的方程．
已知函数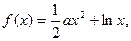
(1)当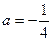
时，求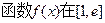
上的最大值、最小值：
(2)求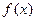
的单调区间；
如图所示，在直三棱柱ABC－A1B1C1中，AB＝1，AC＝AA1＝，∠ABC＝60°.
(1)证明：AB⊥A1C；
(2)求二面角A－A1C－B的余弦值．
某高等学校自愿献血的50位学生的血型分布的情况如下表：
| 血型 |
A |
B |
AB |
O |
| 人数 |
20 |
10 |
5 |
15 |
(1) 从这50位学生中随机选出2人，求这2人血型都为A型的概率；
（2）现有一位血型为A型的病人需要输血，要从血型为A，O的学生中随机选出2人准备献血，记选出A型血的人数为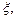
求随机变量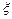
的分布列及数学期
望．
已知sin(π－α)＝，α∈(0，)．
(1)求sin2α－cos2的值；
(2)求函数f(x)＝cosαsin2x－cos2x的单调递增区间．