(本小题满分12分)2011年5月1日,湖北将举行大型活动,在安全保障方面,警方从武警训练基地挑选防爆警察,从体能、射击、反应三项指标进行检测,如果这三项中至少有两项通过即可入选。假定某基地有4名武警战士(分别记为A、B、C、D)拟参加挑选,且每人能通过体能、射击、反应的概率分别为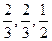 。这三项测试能否通过相互之间没有影响。
。这三项测试能否通过相互之间没有影响。
(1)求A能够入选的概率;
(2)规定:按入选人数得训练经费(每入选1人,则相应的训练基地得到3000元的训练经费),求该基地得到训练经费不大于6000元的概率。
(本小题满分13分)
如图,ABCD是块矩形硬纸板,其中AB=2AD= 2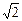 ,E为DC中点,将它沿AE折成直二面角D-AE-B.
,E为DC中点,将它沿AE折成直二面角D-AE-B.
(Ⅰ)求证:AD⊥平面BDE;
(Ⅱ)求二面角B-AD-E的余弦值.
(本小题满分13分)
某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.
(Ⅰ)设所选3人中女生人数为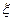 ,求
,求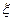 的分布列及数学期望
的分布列及数学期望 ;
;
(Ⅱ)在男生甲被选中的情况下,求女生乙也被选中的概率.
已知函数f (x) = 2cos2x-2sinxcosx + 1.
(1)设方程f (x) – 1 = 0在(0,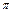 )内的
)内的 两个零点x1,x2,求x1 + x2的值;
两个零点x1,x2,求x1 + x2的值;
(2)把函数y = f (x)的图象 向左平移m (m>0)个单位使所得函数的图象关于点(0,2)对称,求m的最小值.
向左平移m (m>0)个单位使所得函数的图象关于点(0,2)对称,求m的最小值.
(本小题满分14分)
已知函数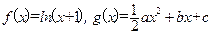 .
.
(1)若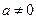 ,曲线
,曲线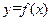 和
和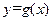 在原点处的切线重合,求实数
在原点处的切线重合,求实数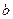 的值.
的值.
(2)若 ,
,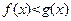 在
在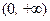 上恒成立,求
上恒成立,求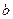 的取值范围.
的取值范围.
(3)函数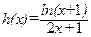 ,在
,在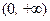 上函数
上函数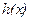 图象与直线y=1是否有交点?若有,求出交点,若没有,请说明理由.
图象与直线y=1是否有交点?若有,求出交点,若没有,请说明理由.
(本小题满分12分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的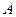 处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以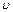 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过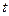 小时与轮船相遇。
小时与轮船相遇。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;