已知过抛物线
的焦点,斜率为
的直线交抛物线于
两点,且
.
(1)求该抛物线的方程;
(2)
为坐标原点,
为抛物线上一点,若
,求
的值.
如图,已知椭圆C的方程为 +y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的矩形的两个顶点.
(1)设P是椭圆C上任意一点,若 =m
=m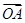 +n
+n ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
(2)若M、N是椭圆C上两个动点,且直线OM、ON的斜率之积等于直线OA、OB的斜率之积,试探求△OMN的面积是否为定值,并说明理由.
给定椭圆C: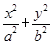 =1(a>b>0),称圆心在原点O、半径是
=1(a>b>0),称圆心在原点O、半径是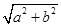 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F(
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F(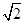 ,0),其短轴的一个端点到点F的距离为
,0),其短轴的一个端点到点F的距离为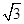 .
.
(1)求椭圆C和其“准圆”的方程;
(2)若点A是椭圆C的“准圆”与x轴正半轴的交点,B、D是椭圆C上的两相异点,且BD⊥x轴,求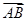 ·
·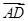 的取值范围;
的取值范围;
(3)在椭圆C的“准圆”上任取一点P,过点P作直线l1,l2,使得l1,l2与椭圆C都只有一个交点,试判断l1,l2是否垂直?并说明理由.
如图,在平面直角坐标系xOy中,圆C:(x+1)2+y2=16,点F(1,0),E是圆C上的一个动点,EF的垂直平分线PQ与CE交于点B,与EF交于点D.
(1)求点B的轨迹方程;
(2)当点D位于y轴的正半轴上时,求直线PQ的方程;
(3)若G是圆C上的另一个动点,且满足FG⊥FE,记线段EG的中点为M,试判断线段OM的长度是否为定值?若是,求出该定值;若不是,说明理由.
如图,过抛物线C:y2=4x上一点P(1,-2)作倾斜角互补的两条直线,分别与抛物线交于点A(x,y1),B(x2,y2).
(1)求y1+y2的值;
(2)若y1≥0,y2≥0,求△PAB面积的最大值.
已知双曲线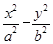 =1的离心率为2,焦点到渐近线的距离等于
=1的离心率为2,焦点到渐近线的距离等于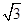 ,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.
(1)求双曲线的方程;
(2)若△F1AB的面积等于6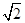 ,求直线l的方程.
,求直线l的方程.