已知数列an与bn满足：bnanan1bn1an2,bn31-优题课

题文

已知数列 $\{a_{n}\}$ 与 $\{b_{n}\}$ 满足： $b_{n} a_{n} + a_{n + 1} + b_{n + 1} a_{n + 2}, b_{n} = \frac{3 + {(- 1)}^{n}}{2}, n \in N^{+}$ ，且 $a_{1} = 2, a_{2} = 4$ ．
（Ⅰ）求 $a_{3}, a_{4}, a_{5}$ 的值；
（Ⅱ）设 $c_{n} = a_{2 n - 1} + a_{2 n + 1}, n \in N^{+}$ ，证明： $\{c_{n}\}$ 是等比数列；
（Ⅲ）设 $S_{k} = a_{2} + a_{4} + \dots + a_{2 k}, k \in N^{+}$ ,证明： $\sum_{K = 1}^{4 n} \frac{S_{k}}{a_{k}} < \frac{7}{6} (n \in N^{+})$ ．

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

一个多面体的直观图、正视图、侧视图、俯视图如图所示，M、N分别为A₁B、B₁C₁的中点.

(1)求证：MN//平面ACC₁A₁；
(2)求证：MN^平面A₁BC.

解答下列问题：
（1）求平行于直线3x+4y-2=0,且与它的距离是1的直线方程；
（2）求垂直于直线x+3y-5=0且与点P(-1,0)的距离是的直线方程.

已知函数.
（1）求函数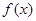的单调区间；
（2）若函数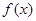满足：
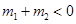①对任意的，，当时，有成立；
②对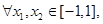恒成立.求实数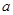的取值范围.

某企业为扩大生产规模，今年年初新购置了一条高性能的生产线，该生产线在使用过程中的设备维修、燃料和动力等消耗的费用（称为设备的低劣化值）会逐年增加，第一年设备低劣化值是4万元，从第二年到第七年，每年设备低劣化值均比上年增加2万元，从第八年开始，每年设备低劣化值比上年增加25%．
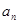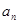（1）设第年该生产线设备低劣化值为，求的表达式；
（2）若该生产线前年设备低劣化平均值为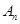,当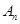达到或超过12万元时，则当年需要更新生产线，试判断第几年需要更新该生产线，并说明理由.

知椭圆的离心率为，定点，椭圆短轴的端点是，且.
（1）求椭圆的方程；
（2）设过点且斜率不为0的直线交椭圆于两点.试问轴上是否存在异于的定点，使平分？若存在，求出点的坐标；若不存在，说明理由.

试卷网试题网古诗词网作文网范文网