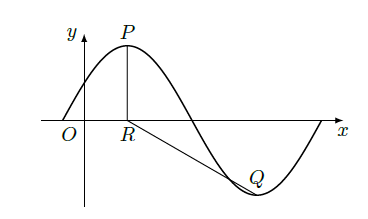
已知函数
的部分图像,如图所示,
分别为该图像的最高点和最低点,点
的坐标为
.
(Ⅰ)求
的最小正周期及
的值;
(Ⅱ)若点 的坐标为 ,
(本小题满分14分)已知函数 有下列性质:“若
有下列性质:“若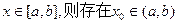 ,使得
,使得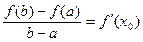 ”成立。
”成立。
(1)利用这个性质证明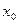 唯一;
唯一;
(2)设A、B、C是函数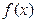 图象上三个不同的点,试判断△ABC的形状,并说明理由。
图象上三个不同的点,试判断△ABC的形状,并说明理由。
(本小题满分12分)已知数列 ,
,
定义其倒均数是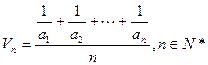 。
。
(1)求数列{ }的倒均数是
}的倒均数是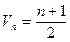 ,求数列{
,求数列{ }的通项公式
}的通项公式 ;
;
(2)设等比数列 的首项为-1,公比为
的首项为-1,公比为 ,其倒数均为
,其倒数均为 ,若存在正整数k,使得当
,若存在正整数k,使得当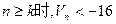 恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
(本小题满分12分)已知空间向量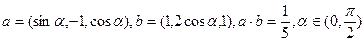
(1)求 及
及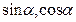 的值;
的值;
(2)设函数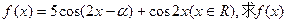 的最小正周期及
的最小正周期及 取得最大值时x的值。
取得最大值时x的值。
如图,四棱锥P—ABCD的底面是正方形,PA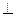 底面ABCD,PA=2,
底面ABCD,PA=2,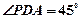 ,
,
点E,F分别为棱AB,PD的中点。
(I)在现有图形中,找出与AF平行的平面,并给出证明;
(II)判断平面PCE与平面PCD是否垂直?若垂直,给出证明;若不垂直,说明理由。
(选修4—1,几何证明选讲)
如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE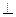 AB,垂足为E,且E是OB的中点,求BC的长。
AB,垂足为E,且E是OB的中点,求BC的长。