有甲、乙两名学生,经统计,他们在解答同一份数学试卷时,各自的成绩在80分、90分、100分的概率分布大致如下表所示:
甲:
| 分数X |
80 |
90 |
100 |
| 概率P |
0.2 |
0.6 |
0.2 |
乙:
| 分数Y |
80 |
90 |
100 |
| 概率P |
0.4 |
0.2 |
0.4 |
试分析两名学生的成绩水平.
某市电力公司在电力供不应求时期,为了居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过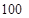 度时,按每度
度时,按每度 元计费,每月用电超过
元计费,每月用电超过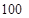 度时,超过部分按每度
度时,超过部分按每度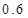 元计费,每月用电超过
元计费,每月用电超过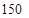 度时,超过部分按每度
度时,超过部分按每度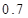 元计费.
元计费.
(1)设每月用电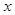 度,应交电费
度,应交电费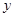 元,写出
元,写出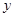 关于
关于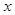 的函数;
的函数;
(2)已知小王家第一季度缴费情况如下:
| 月份 |
1 |
2 |
3 |
合计 |
| 缴费金额 |
87元 |
62元 |
45元8角 |
194元8角 |
问:小王家第一季度共用了多少度电?
已知函数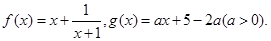
(1)判断函数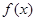 在
在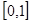 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;
(2)若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数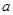 的取值范围.
的取值范围.
已知函数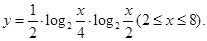
(1)令 ,求
,求 关于
关于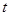 的函数关系式及
的函数关系式及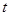 的取值范围;
的取值范围;
(2)求函数的值域,并求函数取得最小值时的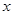 的值.
的值.
已知函数 是定义在
是定义在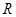 上的奇函数,当
上的奇函数,当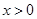 时的解析式为
时的解析式为 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的零点.
的零点.
设集合 是函数
是函数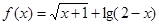 的定义域,集合
的定义域,集合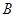 是函数
是函数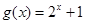 的值域.
的值域.
(1)求集合 ;
;
(2)设集合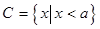 ,若集合
,若集合 ,求实数
,求实数 的取值范围.
的取值范围.