某市电力公司在电力供不应求时期,为了居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过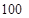 度时,按每度
度时,按每度 元计费,每月用电超过
元计费,每月用电超过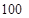 度时,超过部分按每度
度时,超过部分按每度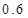 元计费,每月用电超过
元计费,每月用电超过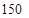 度时,超过部分按每度
度时,超过部分按每度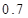 元计费.
元计费.
(1)设每月用电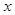 度,应交电费
度,应交电费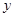 元,写出
元,写出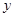 关于
关于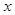 的函数;
的函数;
(2)已知小王家第一季度缴费情况如下:
| 月份 |
1 |
2 |
3 |
合计 |
| 缴费金额 |
87元 |
62元 |
45元8角 |
194元8角 |
问:小王家第一季度共用了多少度电?