如图所示,圆 的直径
的直径 ,
, 为圆周上一点,
为圆周上一点,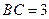 .过
.过 作圆的切线
作圆的切线 ,过
,过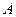 作
作 的垂线
的垂线 ,
, 分别与直线
分别与直线 、圆交于点
、圆交于点 ,求
,求 的度数和线段
的度数和线段 的长。
的长。
已知曲线 的方程为:
的方程为: (
( ,
, 为常数).
为常数).
(1)判断曲线 的形状;
的形状;
(2)设曲线 分别与
分别与 轴、
轴、 轴交于点
轴交于点 、
、 (
( 、
、 不同于原点
不同于原点 ),试判断
),试判断 的面积
的面积 是否为定值?并证明你的判断;
是否为定值?并证明你的判断;
(3)设直线 与曲线
与曲线 交于不同的两点
交于不同的两点 、
、 ,且
,且 ,求曲线
,求曲线 的方程.
的方程.
如图,四棱锥 的底面是正方形,侧棱
的底面是正方形,侧棱 底面
底面 ,过
,过 作
作 垂直
垂直 交
交 于
于 点,作
点,作 垂直
垂直 交
交 于
于 点,平面
点,平面 交
交 于
于 点,且
点,且 ,
, .
.
(1)试证明不论点 在何位置,都有
在何位置,都有 ;
;
(2)求 的最小值;
的最小值;
(3)设平面 与平面
与平面 的交线为
的交线为 ,求证:
,求证: .
.
图是某市 月
月 日至
日至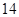 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数( )小于
)小于 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择 月
月 日至
日至 月
月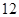 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留 天.
天.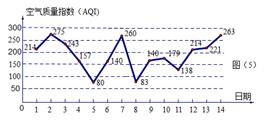
(1)求此人到达当日空气质量优良的概率;
(2)求此人停留期间至多有1天空气重度污染的概率.
已知函数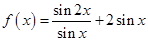 .
.
(1)求函数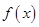 的定义域和最小正周期;
的定义域和最小正周期;
(2)若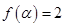 ,
,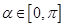 ,求
,求 的值.
的值.
已知函数 .
.
(1)当 且
且 时,证明:
时,证明: ;
;
(2)若对 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 时,证明:
时,证明: .
.