已知函数
（其中
）的图象与x轴的交点中，相邻两个交点之间的距离为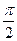
，且图象上一个最低点为
.
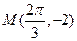(Ⅰ)求
的解析式；（Ⅱ）当
，求的值域
已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点B恰好是抛物线
的焦点，且离心率等于
，直线
与椭圆C交于M，N两点。
（1）求椭圆C的方程；
（2）椭圆C的右焦点F是否可以为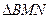
的垂心？若可以，求出直线的方程；若不可以，请说明理由。
已知平行四边形
的顶点
，
，
求顶点
的坐标．
一条河的两岸平行，河的宽度
m，一艘船从
处出发到河对岸．已知船的速度
km/h，水流速度
km/h．要使船行驶的时间最短，那么船行驶的距离与合速度的比值必须最小．此时我们分三种情况讨论：
（１）当船逆流行驶，与水流成钝角时；
（２）当船顺流行驶，与水流成锐角时；
（３）当船垂直于对岸行驶，与水流成直角时．
请同学们计算上面三种情况，是否当船垂直于对岸行驶时，与水流成直角时，所用时间最短
设
，
是平面内一组基底，证明：当
时，恒有
．
如图，已知
，
，任意点
关于点
的对称点为
，点关于点
的对称点为
，用
、
表示向量
．
